Para entender el concepto de número imaginario es necesario recordar algunos aspectos matemáticos previos relativos a la raíz cuadrada de un número o la potenciación del mismo:

Por ejemplo:

(5) * (5) = 5²  que es igual a 25 (número positivo elevado al cuadrado, resultado es positivo)

(–5) * (–5) = –5² que es igual a +25 (número negativo elevado al cuadrado, resultado es positivo)

Entonces, si nos piden calcular la raíz cuadrada de 25, el resultado puede ser + 5 o  –5.

Esto se explica porque, en el ámbito de los números reales, cada raíz cuadrada tiene dos soluciones: Una positiva y otra negativa. Por regla casi general, nos interesamos tan sólo en la solución positiva.

Llevemos ahora nuestro pensamiento a las ecuaciones cuadráticas (o de segundo grado) que ya hemos visto (y cuya solución y fórmula es muy conveniente recordar y repasar aquí de nuevo).

Recordemos que dada la ecuación de segundo grado (o cuadrática) de la forma

ax² + bx + c = 0

Sus soluciones vienen dadas por la fórmula

                                                      
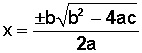
Cualquiera que haya trabajado con ecuaciones cuadráticas, sabe que encontrarse con raíces de números negativos es muy habitual. Por esta razón, los matemáticos inventaron números que no son reales y cuyo cuadrado puede ser un número negativo.

Un ejemplo de ecuación cuadrática sencilla sería:

3x²  + 85 = 0,

la cual podemos resolver en forma directa:

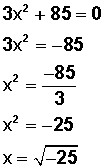
Nota: Esta ecuación también se puede calcular usando la fórmula recordada más arriba, y se llega al mismo resultado.

Hasta ahora, nos dábamos por satisfechos y decíamos que, en esta ecuación, equis es igual a raíz cuadrada de menos 25.

Pero, no es así: resulta que la raíz cuadrada de menos 25 no existe o no se puede calcular.

Claro, la raíz cuadrada de menos 25 no puede ser + 5, ya que (+ 5) * (+ 5)  = + 25 (positivo) y tampoco puede ser – 5, ya que (–5) * (–5)  = + 25 (positivo).

Aquí surge la gran pregunta: ¿es posible obtener o calcular la raíz cuadrada de un número negativo? En otras palabras ¿existen números reales que multiplicados por sí mismos arrojen un resultado negativo?

En los números reales no existen, pero actualmente podemos decir que se encontraron, gracias al matemático italiano Cardano, a quien se le ocurrió que “permitir” la existencia de raíces cuadradas de números negativos posibilitaba resolver cualquier ecuación cuadrática.

Pero, como ya vimos que no existen números reales cuyos cuadrados sean negativos, estos números “inventados” fueron llamados números “imaginarios”.

Notas:

También se aplican los números imaginarios a las raíces negativas de índice par.

En algunas fuentes se hacen sinónimos números imaginarios con números complejos,  pero luego veremos que hay una diferencia.

Definición

Ahora, podemos aventurar una definición para los números imaginarios:

Los números imaginarios son la representación de números que elevados al cuadrado terminan con signo negativo.

Así:

Representan “números imaginarios”, que necesitan un pequeño ajuste para mostrarse como tales y ser soluciones definitivas en cualquier ecuación donde aparezcan:

La preocupación por estas raíces de signo negativo empezó en 1777 cuando el matemático y físico suizo Leonhard Euler bautizó la raíz de –1 con la letra i (por lo de imaginario).

Lo cual se escribe como:

que se convirtió en la unidad de los números imaginarios.

Volvamos a nuestro ejemplo anterior:

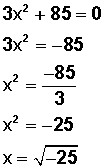
Veamos en qué consiste el pequeño ajuste de que hablamos, para obtener las soluciones definitivas (con números imaginarios) a nuestra ecuación:

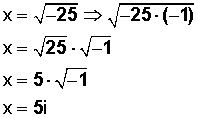
¿Qué hicimos?

La raíz cuadrada del número negativo – 25 la expresamos como raíz cuadrada del mismo número, pero positivo (ya que lo expresamos como –25 por  –1) , y luego la multiplicamos por la unidad imaginaria

Y tenemos el resultado definitivo para nuestra ecuación:

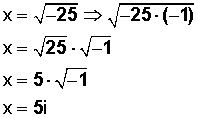
x = 5i (número imaginario)

Entonces,

2i, 3i, 4i, 5i,  6i, son números imaginarios.

Hay que anotar que la unidad imaginaria (i) se puede multiplicar por si misma dando lugar a diferentes potencias, las cuales son:

i⁰ = 1

i¹ = i

i² = –1

i³ = –i

i⁴ = 1

A partir de aquí, señalemos que el valor de las potencias de la unidad imaginaria se empieza a repetir de cuatro en cuatro.

Entonces, para conocer el valor de una determinada potencia de i, se divide el exponente entre 4, y el resto es el exponente de la potencia con su equivalente, según vimos arriba.

Por ejemplo, si tenemos un i²³, dividimos 23 entre 4 y el resultado es 5, pero queda un resto de 3.  Entonces esa i equivale a i³ que es igual a –i.

Aclarado el concepto de número imaginario, veamos a continuación los

Números complejos