Números reales |
Se representan con la letra
.
El conjunto de los Números Reales (
) está integrado por:
• El conjunto de los
Números Racionales
(
) que corresponden a la unión de todos los números cuya
expresión decimal
es
finita, infinita periódica
o
infinita semiperiódica.
• El conjunto de los números enteros , positivos y negativos, más el cero
• El conjunto de los Números Irracionales (I) que está formado por la unión de todos los números que admiten una expresión infinita no periódica.
Entonces, se llaman
Números Reales
a
todos aquellos que se pueden expresar en forma decimal finita o infinita; es decir, el conjunto de los Números Reales (
) está formado por los elementos del conjunto
unido con
I
.
El siguiente cuadro es ilustrativo: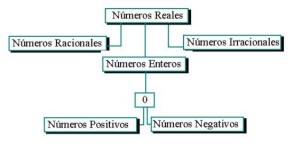
|
Todos los números reales pueden ser representados en la recta numérica.
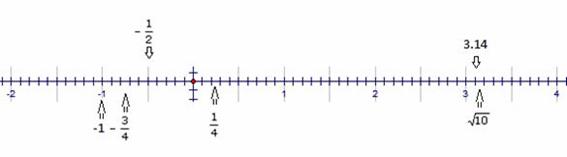
A cada punto de la recta numérica le corresponde un número real y viceversa; es decir, existe una correspondencia uno a uno entre los puntos de la recta numérica y los números reales.
Importante:
Con números reales pueden realizarse todo tipo de operaciones básicas con dos excepciones importantes:
1.- No existen raíces de orden par (cuadradas, cuartas, sextas, etc.) de números negativos en números reales, razón por la cual existe el conjunto de los números complejos donde estas operaciones sí están definidas.
2.- No existe la división entre cero , pues carece de sentido dividir entre nada o entre nadie; es decir, no existe la operación de dividir entre nada.
En otras palabras, no son reales las fracciones con denominador cero y las raíces de índice par y radicando negativo.
Infinito no es un número real
Infinito no es un número real, es una idea. Una idea de algo que no termina.
Recuerde, además, que cualquier fracción con numerador cero, tiene como resultado final, el cero (cero dividido cualquier cosa es igual a cero)
Ver: PSU: Matemática, Pregunta 36_2010
ir a: Operaciones aritméticas y propiedades con números reales
Ir a: Conjuntos numéricos
Fuentes Internet:
http://es.wikipedia.org/wiki/N%C3%BAmero_real
http://wmatem.eis.uva.es/~matpag/CONTENIDOS/Reales/marco_reales.htm