En estadística , la distribución binomial es una distribución de probabilidad discreta que indica el número de éxitos al realizar una secuencia de n ensayos independientes entre sí, con una probabilidad fija (p) de ocurrencia del éxito entre esos ensayos.

Una variable discreta es aquella que solo puede tomar un número finito de valores entre dos valores cualesquiera de una característica.

La función de probabilidad de la distribución binomial, también denominada función de la distribución de Bernoulli , se expresa con la fórmula:

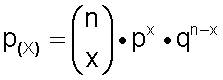
Donde:

n es el número de pruebas o ensayos .

x es el número esperado de éxitos .

p es la probabilidad porcentual de éxito .

q es la probabilidad porcentual de fracaso, que se obtiene siempre haciendo 1 – p.

Nota:

Hay que observar que las probabilidades de éxito y fracaso son complementarias; es decir, q = 1 – p y p = 1 – q , por lo que basta saber una de ellas para calcular la otra.

El coeficiente binomial

, también llamado número combinatorio , se puede expresar como

nCx.

El cálculo del coeficiente binomial se obtiene con la fórmula

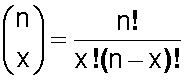
Al incluir n! incorporamos el concepto de función factorial , el que se puede ver en Factorial o Función factorial .

Ahora, veamos algunos ejemplos o ejercicios que nos permitirán entender mejor esta operatoria matemática llamada distribución binomial.

Ejercicio

El 80 % de un universo potencial ha visto un exitoso programa de televisión. Al juntarse 4 amigas aficionadas al tema:

¿Cuál es la probabilidad de que 2 amigas del grupo hayan visto el programa?

Datos que tenemos:

n = 4  (total de la muestra)

p = 0,8  (porcentaje unitario de éxito) se obtiene a partir del 80% conocido

q = 0,2  (porcentaje unitario de fracaso) (se obtiene haciendo 1 – 0,8 = 0,2

x = 2 (amigas que hayan visto el programa)

Apliquemos nuestra fórmula conocida y pongamos los datos que tenemos:

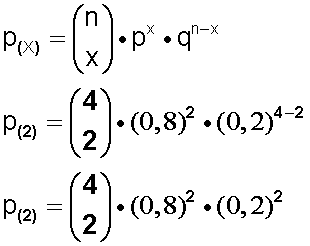
Calculemos el coeficiente binomial:

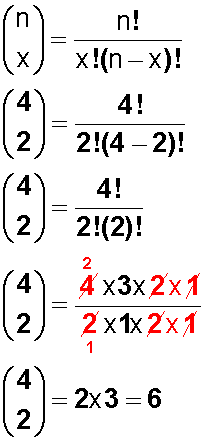
Y hacemos el cálculo:

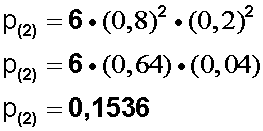
Lo que expresado como porcentaje nos dice que hay 15,36 % de posibilidades de que entre las 4 amigas, 2 hayan visto el programa.

¿Y cuál es la posibilidad de que, como máximo, lo hayan visto 2 amigas?

Para resolver esta opción debemos fijarnos en que la condición ahora es que “como máximo” lo hayan visto 2, lo cual implica que también puede haberlo visto 1 persona o cero persona.  Esto nos indica que  x puede tener 3 valores  x = (0, 1, 2).

En este caso, aplicamos la fórmula para cada opción de x y las sumamos entre sí:

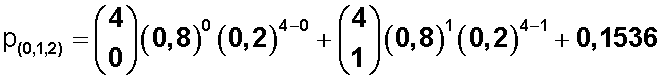
Nota: 0,1536 es el porcentraje obtenido en el punto 1, que indica la probabilidd de que 2 amigas lo hayan visto .

Calculemos los coeficientes binomiales:

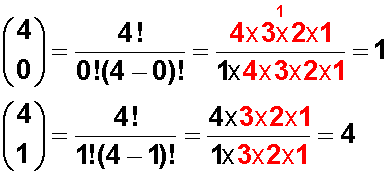
Entonces:

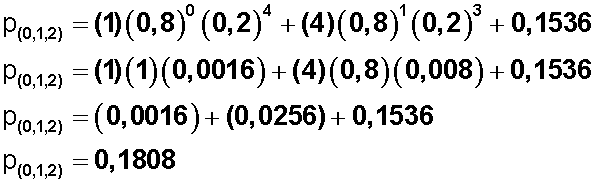
Expresado en porcentaje, significa que hay 18,08 % de probabilidad que el programa haya sido visto como máximo por 2 de las 4 amigas (pueden ser 0, 1 o 2).

Para ver otros ejercicios, ir a:

Distribución binomial, Ejercicios001

Distribución binomial, Ejercicios002