La probabilidad de que un aparato de televisión, antes de revisarlo, sea defectuoso, es de 0,12.

Si se revisan 5 aparatos:

Calcule

a) la probabilidad de que 2 sean defectuosos

Veamos los datos que tenemos:

p = 0,12  (probabilidad de que uno sea defectuoso)

q = 1 - 0,12

q = 0,88  (probabilidad de que uno no sea defectuoso)

n = 5 (total de tv que se revisan)

x = 2 (aparatos defectuosos es la condición)

Usamos la fórmula

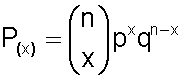
Y sustituimos los valores:

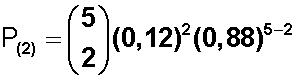
Ahora calculamos el coeficiente binomial con la fórmula:

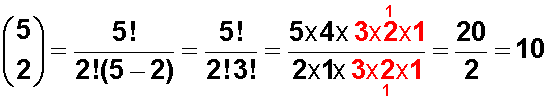
Y completamos la fórmula inicial:

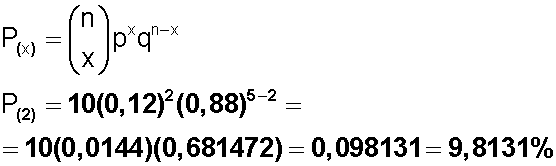
Si se revisan 5 aparatos, la probabilidad de que 2 sean defectuosos es del 9,8131 %.

Calcule

b) la probabilidad de que menos de 3 sean defectuosos

La fórmula es la misma

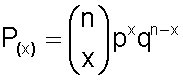
Y los valores son los mismos, salvo que ahora la x puede tener 3 valores (0, 1 ,2) (por que el enunciado dice “menos de 3” ).

Reemplazamos los valores de x (0, 1,2) y los sumamos:

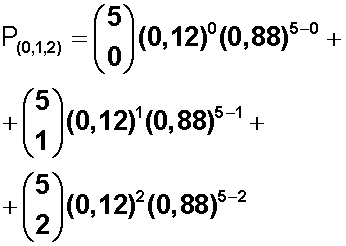
Coeficiente binomial

Calculamos el Coeficiente binomial para 0 (cero) aparato y para 1 (uno), el coeficiente para 2 aparatos lo tenemos arriba y es 10.

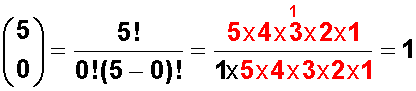
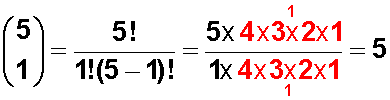
Reemplazamos por los valores de los coeficientes binomiales:

Nótese que para el coeficiente 2 colocamos el resultado anterior (0,0981)

Hacemos los cálculos y nos queda:

Hay 98,56 % de probabilidad de que al revisar 5 aparatos, encontremos menos de 3 defectuosos.

Nota para recordar:

0! Es igual a 1 (por convención)

(0,12) ⁰ es igual a 1 (potencias)

Calcule

c) la probabilidad de que al menos 3 sean defectuosos

Y los valores son los mismos, salvo que ahora la x puede tener 3 valores (3, 4, 5) (por que el enunciado dice “al menos 3” , por lo que pueden ser 3, 4 o 5 los defectuosos).

Podemos hacer lo mismo que en el cálculo anterior reemplazado los valores de x (3,4,5).

Pero podemos usar un atajo, usando la fórmula del “complemento” .

Donde ya conocemos p _(A) , pues lo calculamos en el punto anterior y significa que sabemos la probabilidad para cuando x = (0, 1, 2) que es igual a 0,9856 que equivale al 98,56 %

Entonces, como el universo de la muestra es 5, el complemento  a 0, 1, 2 será P(3, 4, 5)

Aplicamos la fórmula y queda

p _{(3, 4, 5)} = 1 - 0,9856 = 0,0144 = 1,44 %

Entonces la probabilidad de que al menos 3 (pudiendo ser 3, 4 o 5 ) sean defectuosos es de 1,44%.

Calcule

d) la probabilidad de que ninguno sea defectuoso

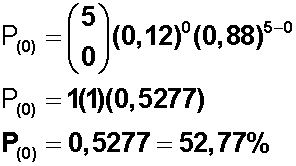
Revisados 5 aparatos, la probabilidad de que ninguno sea defectuoso es del 52,77 %

Calcule

e) la probabilidad de que alguno sea defectuoso.

En este caso, “alguno defectuoso” debe entenderse como que 1, 2, 3, 4 o 5 pueden ser defectuosos. Podríamos calcular con P (x)  = (1, 2, 3, 4, 5).

Pero podemos usar el complemento de P _(1,2,3,4,5) que es P ₍₀₎ que calculamos arriba en la opción d) donde la probabilidad de que ninguno sea defectuoso es 0,5277 equivalente al 52,77 %.

Entonces:

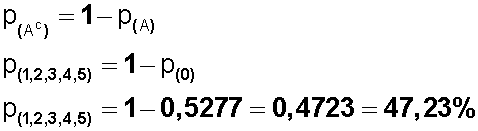
La probabilidad de que alguno sea defectuoso es del 47,23%.

Calcule

f) El número de televisores defectuosos que se encontrarán por término medio.

Si la posibilidad de que un aparato sea defectuoso es de 0,12, la posibilidad de que 100 sean defectuosos es del 12 %. Expresado en fracción sería 12/100, la cual podemos simplificar a 6/50 y luego a 3/25.

Entonces, significa que se encontrarán 3 televisores defectuosos cada 25 revisados.

Volver a:

Distribución  binomial

Ir a:

Ejercicios de distribución binomial 2

Fuente Internet

https://www.youtube.com/watch?v=OWDIFqB5ZZY

Ver en Internet:

http://agrega.educacion.es/repositorio/12062012/1e/es_2012061212_9235109/bach_problemas_sobre_la_distribucion_binomial/problemas_binomial/actividad.html

En you tube

https://www.youtube.com/watch?v=EisaSQ1j_Kk