Estadística |
La palabra "estadística" suele utilizarse bajo dos significados distintos:
1º Como colección de datos numéricos .
Esto es el significado más vulgar de la palabra estadística. Se sobrentiende que dichos datos numéricos han de estar presentados de manera ordenada y sistemática. Una información numérica cualquiera puede no constituir una estadística, para merecer este apelativo, los datos han de constituir un conjunto coherente, establecido de forma sistemática y siguiendo un criterio de ordenación.
2º Como ciencia.
En este significado, la Estadística estudia el comportamiento de los fenómenos de masas. Como todas las ciencias, busca las características generales de un colectivo y prescinde de las particulares de cada elemento. Así por ejemplo al investigar el sexo de los nacimientos, iniciaremos el trabajo tomando un grupo numeroso de nacimientos y obtener después la proporción de varones.
(Ver: Tipos de estadísticas )
Es muy frecuente enfrentarnos con fenómenos en los que es muy difícil predecir el resultado; así, no podemos dar una lista con las personas que van a morir con una cierta edad, o el sexo de un nuevo ser hasta que transcurra un determinado tiempo de embarazo.
Por tanto, el objetivo de la estadística es hallar las regularidades que se encuentran en los fenómenos de masa.
(Ver Historia de la Estadística )
Población, elementos y caracteres.
Es obvio que todo estudio estadístico ha de estar referido a un conjunto o colección de personas o cosas. Este conjunto de personas o cosas es lo que denominaremos población.
Las personas o cosas que forman parte de la población se denominan elementos. En sentido estadístico un elemento puede ser algo con existencia real, como un automóvil o una casa, o algo más abstracto como la temperatura, un voto, o un intervalo de tiempo.
A su vez, cada elemento de la población tiene una serie de características que pueden ser objeto del estudio estadístico. Así por ejemplo si consideramos como elemento a una persona, podemos distinguir en ella los siguientes caracteres:
Sexo, Edad, Nivel de estudios, Profesión, Peso, Altura, Color de pelo, etc.
Luego por tanto de cada elemento de la población podremos estudiar uno o más aspectos cualidades o caracteres.
La población puede ser según su tamaño de dos tipos:
Población finita: cuando el número de elementos que la forman es finito, por ejemplo el número de alumnos de un centro de enseñanza, o grupo clase.
Población infinita: cuando el número de elementos que la forman es infinito, o tan grande que pudiesen considerarse infinitos. Como por ejemplo si se realizase un estudio sobre los productos que hay en el mercado. Hay tantos y de tantas calidades que esta población podría considerarse infinita.
Ahora bien, normalmente en un estudio estadístico no se puede trabajar con todos los elementos de la población sino que se realiza sobre un subconjunto de la misma.
Este subconjunto puede ser una muestra , cuando se toman un determinado número de elementos de la población, sin que en principio tengan nada en común; o una subpoblación , que es el subconjunto de la población formado por los elementos de la población que comparten una determinada característica, por ejemplo de los alumnos del centro la subpoblación formada por los alumnos de 3º Medio o la subpoblación de los varones.
Variables y atributos.
Como hemos visto, los caracteres de un elemento pueden ser de muy diversos tipos, por lo que los podemos clasificar en: dos grandes clases:
Variables Cuantitativas.
Variables Cualitativas o Atributos.
Las variables cuantitativas son las que se describen por medio de números, como por ejemplo el peso, altura, edad, número de suspendidos…
A su vez este tipo de variables se puede dividir en dos subclases:
- Cuantitativas discretas . Aquellas a las que se les puede asociar un número entero, es decir, aquellas que por su naturaleza no admiten un fraccionamiento de la unidad, por ejemplo número de hermanos, páginas de un libro, etc.
- Cuantitativas continuas : Aquellas que no se pueden expresar mediante un número entero, es decir, aquellas que por su naturaleza admiten que entre dos valores cualesquiera la variable pueda tomar cualquier valor intermedio, por ejemplo peso, tiempo. etc.
No obstante en muchos casos el tratamiento estadístico hace que a variables discretas las trabajemos como si fuesen continuas y viceversa.
Los atributos son aquellos caracteres que para su definición precisan de palabras, es decir, no le podemos asignar un número. Por ejemplo sexo, profesión, estado civil, etc.
A su vez las podemos clasificar en:
- Ordenables: Aquellas que sugieren una ordenación, por ejemplo la graduación militar, el nivel de estudios, etc.
- No ordenables: Aquellas que sólo admiten una mera ordenación alfabética, pero no establece orden por su naturaleza, por ejemplo el color de pelo, sexo, estado civil, etc.
Distintos Tipos de Frecuencia:
Una de los primeros pasos que se realizan en cualquier estudio estadístico es la tabulación de resultados, es decir, recoger la información de la muestra resumida en una tabla en la que a cada valor de la variable se le asocian determinados números que representan el número de veces que ha aparecido, su proporción con respecto a otros valores de la variable, etc. Estos números se denominan frecuencias : Así tenemos los siguientes tipos de frecuencia:
Frecuencia absoluta:
La frecuencia absoluta de una variable estadística es el número de veces que aparece en la muestra dicho valor de la variable, la representaremos por n i
Frecuencia relativa:
La frecuencia absoluta, es una medida que está influida por el tamaño de la muestra, al aumentar el tamaño de la muestra aumentará también el tamaño de la frecuencia absoluta. Esto hace que no sea una medida útil para poder comparar. Para esto es necesario introducir el concepto de frecuencia relativa , que es el cociente entre la frecuencia absoluta y el tamaño de la muestra. La denotaremos por f i
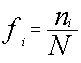
Donde N = Tamaño de la muestra
Ver: PSU: Estadística; Pregunta 05_2006
Frecuencia Absoluta Acumulada:
Para poder calcular este tipo de frecuencias hay que tener en cuenta que la variable estadística ha de ser cuantitativa o cualitativa ordenable. En otro caso no tiene mucho sentido el cálculo de esta frecuencia. La frecuencia absoluta acumulada de un valor de la variable, es el número de veces que ha aparecido en la muestra un valor menor o igual que el de la variable y lo representaremos por N i .
Frecuencia Relativa Acumulada:
Al igual que en el caso anterior la frecuencia relativa acumulada es la frecuencia absoluta acumulada dividido por el tamaño de la muestra, y la denotaremos por F i
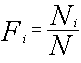
Porcentaje Acumulado:
Análogamente se define el Porcentaje Acumulado y lo vamos a denotar por P i como la frecuencia relativa acumulada multiplicada por 100.
![]()
Ejemplo :
Cuando se manejan conjuntos extensos de datos, el procedimiento preliminar más adecuado consiste en distribuirlos en clases o categorías de acuerdo con el número de casos que pertenecen a cada una de dichas clases.
Por ejemplo, se quiere estudiar el puntaje que alcanzan los alumnos universitarios en la asignatura de Educación Física. La escala de notas va del 0% al 100%, obteniéndose la siguiente colección de valores:
75- 82 - 68 - 90 - 62 - 88 - 88 - 73
60- 93 - 71 - 59 - 75 - 87 - 74 - 62
95- 78 - 82 - 75 - 94 - 77 - 69 - 74
89- 83 - 75 - 95 - 60 - 79 - 97 - 97
78- 85 - 76 - 65 - 73 - 67 - 88 - 78
62- 76 - 73 - 81 - 72 - 63 - 76 - 75
Para facilitar el análisis de los datos, éstos se ordenan en forma creciente, es decir, de menor a mayor (también puede ordenarse en forma decreciente).
El modo más sencillo de agrupar los datos, es mediante una tabla de datos, que indique, para cada uno de los valores de la colección, el número de veces que aparece, es decir, su frecuencia de aparición .
Distribuciones de frecuencia
Frecuencia absoluta (n i ) : corresponde al número de veces que se observa dicho valor, o en otras palabras al número de veces que se presenta un cierto dato.
Para agrupar los datos por su frecuencia, se deben seguir los siguientes pasos:
1) Se ordenan los datos en orden creciente o decreciente.
2) Se cuenta la frecuencia absoluta de cada valor (cuántas veces se repite cada magnitud)
De acuerdo a los datos anteriores, se observa que el número menor es 59 y el número mayor es 97.
|
Puntaje |
Frecuencia absoluta (n i ) |
|
59 |
1 |
|
60 |
2 |
|
61 |
0 |
|
62 |
3 |
|
63 |
1 |
|
64 |
0 |
|
65 |
1 |
|
66 |
0 |
|
67 |
1 |
|
68 |
1 |
|
69 |
1 |
|
70 |
0 |
|
71 |
1 |
|
72 |
1 |
|
73 |
3 |
|
74 |
2 |
|
75 |
5 |
|
76 |
3 |
|
77 |
1 |
|
78 |
3 |
|
79 |
1 |
|
80 |
0 |
|
81 |
1 |
|
82 |
2 |
|
83 |
1 |
|
84 |
0 |
|
85 |
1 |
|
86 |
0 |
|
87 |
1 |
|
88 |
3 |
|
89 |
1 |
|
90 |
1 |
|
91 |
0 |
|
92 |
0 |
|
93 |
1 |
|
94 |
1 |
|
95 |
2 |
|
96 |
0 |
|
97 |
2 |
|
Frecuencia total |
(N) 48 |
La Tabla de distribución de frecuencias hecha anteriormente sirve para facilitar el estudio de los valores estadísticos. El puntaje corresponde a la variable estadística (primera columna) y las veces que se repite la variable (segunda columna), a la frecuencia absoluta.
Frecuencia total (F): corresponde la suma de las frecuencias absolutas de cada uno de los valores de la variable.
Una vez que se ha construido
Frecuencia absoluta Acumulada ( N i ) : es la suma de las frecuencias absolutas de cada intervalo. La frecuencia acumulada hasta el último intervalo es igual a la frecuencia total de toda la distribución.
Si se amplía
|
Puntaje |
Frecuencia absoluta ( n i ) |
Frecuencia absoluta acumulada ( N i ) |
|
59 |
1 |
1 |
|
60 |
2 |
3 |
|
61 |
0 |
3 |
|
62 |
3 |
6 |
|
63 |
1 |
7 |
|
64 |
0 |
7 |
|
65 |
1 |
8 |
|
66 |
0 |
8 |
|
67 |
1 |
9 |
|
68 |
1 |
10 |
|
69 |
1 |
11 |
|
70 |
0 |
11 |
|
71 |
1 |
12 |
|
72 |
1 |
13 |
|
73 |
3 |
16 |
|
74 |
2 |
18 |
|
75 |
5 |
23 |
|
76 |
3 |
26 |
|
77 |
1 |
27 |
|
78 |
3 |
30 |
|
79 |
1 |
31 |
|
80 |
0 |
31 |
|
81 |
1 |
32 |
|
82 |
2 |
34 |
|
83 |
1 |
35 |
|
84 |
0 |
35 |
|
85 |
1 |
36 |
|
86 |
0 |
36 |
|
87 |
1 |
37 |
|
88 |
3 |
40 |
|
89 |
1 |
41 |
|
90 |
1 |
42 |
|
91 |
0 |
42 |
|
92 |
0 |
42 |
|
93 |
1 |
43 |
|
94 |
1 |
44 |
|
95 |
2 |
46 |
|
96 |
0 |
46 |
|
97 |
2 |
48 |
|
Frecuencia total |
(N) 48 |
La frecuencia absoluta acumulada sirve para responder, por ejemplo, la siguiente pregunta: ¿Cuántos alumnos obtuvieron nota inferior a 80?; la respuesta es 31 alumnos.
Frecuencia relativa ( f i ) : >corresponde a la razón (división) entre la frecuencia absoluta (n i ) y el número total (N) de individuos de la población.
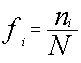
|
Puntaje |
Frecuencia absoluta ( n i ) |
Frecuencia absoluta acumulada ( N i ) |
Frecuencia relativa ( f i ) |
|
59 |
1 |
1 |
0,02083 (1 : 48) |
|
60 |
2 |
3 |
0,0416 (2 : 48) |
|
61 |
0 |
3 |
0 |
|
62 |
3 |
6 |
0,0625 |
|
63 |
1 |
7 |
0,02083 |
|
64 |
0 |
7 |
0 |
|
65 |
1 |
8 |
0,02083 |
|
66 |
0 |
8 |
0 |
|
67 |
1 |
9 |
0,02083 |
|
68 |
1 |
10 |
0,02083 |
|
69 |
1 |
11 |
0,02083 |
|
70 |
0 |
11 |
0 |
|
71 |
1 |
12 |
0,02083 |
|
72 |
1 |
13 |
0,02083 |
|
73 |
3 |
16 |
0,0625 |
|
74 |
2 |
18 |
0,0416 |
|
75 |
5 |
23 |
0,10416 |
|
76 |
3 |
26 |
0,0625 |
|
77 |
1 |
27 |
0,02083 |
|
78 |
3 |
30 |
0,0625 |
|
79 |
1 |
31 |
0,02083 |
|
80 |
0 |
31 |
0 |
|
81 |
1 |
32 |
0,02083 |
|
82 |
2 |
34 |
0,0416 |
|
83 |
1 |
35 |
0,02083 |
|
84 |
0 |
35 |
0 |
|
85 |
1 |
36 |
0,02083 |
|
86 |
0 |
36 |
0 |
|
87 |
1 |
37 |
0,02083 |
|
88 |
3 |
40 |
0,0625 |
|
89 |
1 |
41 |
0,02083 |
|
90 |
1 |
42 |
0,02083 |
|
91 |
0 |
42 |
0 |
|
92 |
0 |
42 |
0 |
|
93 |
1 |
43 |
0,02083 |
|
94 |
1 |
44 |
0,02083 |
|
95 |
2 |
46 |
0, 0416 |
|
96 |
0 |
46 |
0 |
|
97 |
2 |
48 |
0,0416 |
|
Frecuencia total |
(N) 48 |
1 |
La suma de las frecuencias relativas es 1
Frecuencia relativa porcentual: es la frecuencia relativa expresada en porcentajes (%)
|
P i |
= |
f i |
● |
100 |
|
N |
|
Puntaje |
( n i ) |
( N i ) |
( f i ) |
% ( P i %) |
|
59 |
1 |
1 |
0,02083 (1 : 48) |
2,083 |
|
60 |
2 |
3 |
0,0416 (2 : 48) |
4,16 |
|
61 |
0 |
3 |
0 |
0 |
|
62 |
3 |
6 |
0,0625 |
6,25 |
|
63 |
1 |
7 |
0,02083 |
2,083 |
|
64 |
0 |
7 |
0 |
0 |
|
65 |
1 |
8 |
0,02083 |
2,083 |
|
66 |
0 |
8 |
0 |
0 |
|
67 |
1 |
9 |
0,02083 |
2,083 |
|
68 |
1 |
10 |
0,02083 |
2,083 |
|
69 |
1 |
11 |
0,02083 |
2,083 |
|
70 |
0 |
11 |
0 |
0 |
|
71 |
1 |
12 |
0,02083 |
2,083 |
|
72 |
1 |
13 |
0,02083 |
2,083 |
|
73 |
3 |
16 |
0,0625 |
6,25 |
|
74 |
2 |
18 |
0,0416 |
4,16 |
|
75 |
5 |
23 |
0,10416 |
10,416 |
|
76 |
3 |
26 |
0,0625 |
6,25 |
|
77 |
1 |
27 |
0,02083 |
2,083 |
|
78 |
3 |
30 |
0,0625 |
6,25 |
|
79 |
1 |
31 |
0,02083 |
2,083 |
|
80 |
0 |
31 |
0 |
0 |
|
81 |
1 |
32 |
0,02083 |
2,083 |
|
82 |
2 |
34 |
0,0416 |
4,16 |
|
83 |
1 |
35 |
0,02083 |
2,083 |
|
84 |
0 |
35 |
0 |
0 |
|
85 |
1 |
36 |
0,02083 |
2,083 |
|
86 |
0 |
36 |
0 |
0 |
|
87 |
1 |
37 |
0,02083 |
2,083 |
|
88 |
3 |
40 |
0,0625 |
6,25 |
|
89 |
1 |
41 |
0,02083 |
2,083 |
|
90 |
1 |
42 |
0,02083 |
2,083 |
|
91 |
0 |
42 |
0 |
0 |
|
92 |
0 |
42 |
0 |
0 |
|
93 |
1 |
43 |
0,02083 |
2,083 |
|
94 |
1 |
44 |
0,02083 |
2,083 |
|
95 |
2 |
46 |
0, 0416 |
4,16 |
|
96 |
0 |
46 |
0 |
0 |
|
97 |
2 |
48 |
0,0416 |
4,16 |
|
Frecuencia total |
(N) 48 |
1 |
100 % |
En el ejemplo el rango de los datos es:
Rango: 97 - 59 = 38
Rango: Corresponde a la diferencia (resta) entre el mayor y el menor de los datos
Fuente Internet:
http://thales.cica.es/rd/Recursos/rd97/UnidadesDidacticas/53-1-u-punt14.html

