La función factorial de un número entero positivo (n) se define en principio como el producto de todos los números enteros positivos desde 1 (es decir, los números naturales) hasta n, o desde n hasta 1, según el uso.

Esta función factorial se representa con un signo de exclamación “!” puesto a la derecha del número de que se trate.

Este signo de exclamación señala que se deben multiplicar todos los números enteros positivos que hay entre ese número y el 1, ambos incluidos.

Por ejemplo:

A este número, 5! le llamamos generalmente “5 factorial” , aunque también es correcto decir “factorial de 5” .

En las calculadoras científicas hay una tecla con “n!” o “x!” , con ella se puede calcular directamente el factorial de cualquier número.

Otros ejemplos de factoriales:

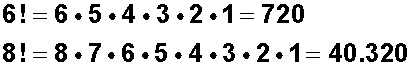
Como vemos, entre mayor es el número el resultado es cada vez es más grande; pero ¿qué hacemos con los números más pequeños?

Por ejemplo:

1! = 1, ya que 1 por 1 = 1

Otra pregunta que podemos hacernos: ¿podemos calcular el 0 factorial?

Evidentemente no tiene sentido, ya que deberíamos multiplicar 0 por 1, lo cual da cero.

Para solucionar esto, se ha convenido entre los matemáticos, y nos incluimos en el convenio, de que el 0 factorial sea igual a 1.

Entonces, no hay que olvidar:

0! = 1

Utilidad de los factoriales

Esta operación factorial o función factorial es muy útil al calcular distribuciones, combinaciones y permutaciones de probabilidades .

Ver:

Distribución binomial de probabilidades

Permutaciones y combinaciones

Ver, además:

http://www.disfrutalasmatematicas.com/numeros/factorial.html