Combinatoria |
La combinatoria es una rama de las matemáticas discretas que trabaja con conjuntos finitos de objetos, de proposiciones, de acciones o de elementos que pueden ser combinados u ordenados.
Matemáticas discretas
Es la base de todo lo relacionado con los números naturales o conjuntos numerables, y estudia procesos que sean contables, donde todos los elementos del conjunto pueden ser contados por separado, uno por uno, usando como base los números enteros. No se utilizan números decimales ni aproximaciones .
Recordemos que un conjunto es una agrupación de elementos ( proposiciones , números, cosas, animales y personas, entre otros) que son bien definidos; es decir, que existe una relación según la cual cada elemento pertenece a un conjunto, y se expresa, por ejemplo, a ∈ A (a pertenece a A).
¿Qué es una proposición en matemáticas discretas?
Una proposición es la posibilidad de la ocurrencia de un hecho, o la necesidad de una acción, o una orden, un deber, una interrogante, etcétera. Una proposición es una sentencia declarativa que debe ser verdadera o falsa, pero no ambas.
Entonces, de un modo general, diremos que la Combinatoria es la parte de las Matemáticas que estudia las diversas formas de realizar agrupaciones con los elementos de un conjunto, formándolas y calculando su número.
Existen distintas maneras de realizar estas agrupaciones: según se consideren todos los elementos de que disponemos o solo algunos, según si influye o no el orden de colocación de los elementos y según se repitan o no los elementos.
Según estas variables, un problema de combinatoria puede ser una combinación , una variación o una permutación , cada una con opción de repetición o sin repetición.
Para continuar en la comprensión de esta materia, es necesario manejar el concepto de factorial y el de número combinatorio , necesarios para el estudio de las combinaciones, las variaciones y las permutaciones.
Ahora, analiza el siguiente mapa conceptual:
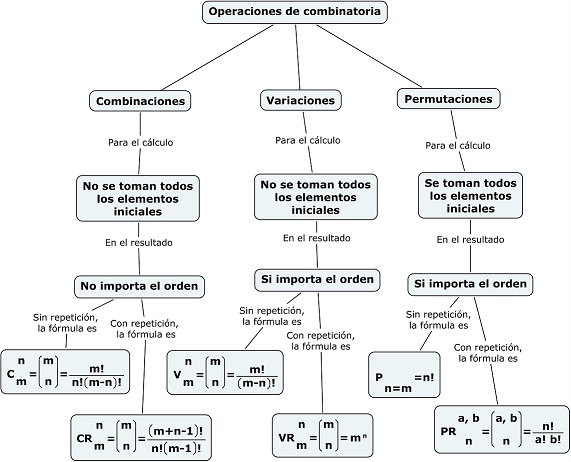
Para definir de qué tipo de operación Combinatoria se trata, hay que hacerse 3 preguntas:
1.- ¿Se toman todos los elementos iniciales?
2.- ¿Importa el orden en el resultado?
3.- ¿Hay repetición de elementos?
El mapa conceptual de arriba entrega las respuestas, e indica cuál es la fórmula que debe usarse.
Combinación
Veamos qué es una Combinación:
Si para obtener el resultado de una agrupación de elementos se considera solo la inclusión de algunos elementos del conjunto, sin importar el orden, estamos hablando de una combinación , que puede obtenerse con repetir elementos o sin repetir elementos.
La expresión numérica de tales combinaciones recibe el nombre de número combinatorio o coeficiente binómico o binomial .
Coeficientes binómicos o binomiales
Se define número combinatorio o coeficiente binómico como el valor numérico de las combinaciones ordinarias (sin repetición) de un conjunto de m elementos (la totalidad) tomados en grupos de n elementos, siendo m y n dos números enteros y positivos tales que m sea mayor o igual a n .
Entonces, un número combinatorio está formado por dos números enteros positivos, m y n , que se colocan uno debajo del otro y encerrados por un paréntesis, como lo vemos abajo:
![]()
Lo único a tener en cuenta, además de que deben ser números enteros positivos, es que el número de arriba (m) no puede ser más pequeño que el de abajo (n); es decir, que debe ser siempre
(m mayor o igual que n).
Ejemplo
Son números combinatorios:
![]()
La fórmula que permite hallar el valor de un número combinatorio, sin repetición de elementos, es la siguiente:
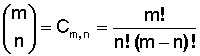
Ojo:
Para entender esta fórmula y trabajar en Combinatoria es imprescindible estudiar y dominar el tema Función factorial en:
http://www.profesorenlinea.cl/matematica/Factorial.html
Continuando con nuestro ejemplo, este se desarrolla así:
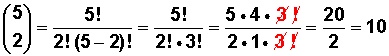
10 es el resultado del número combinatorio
![]()
Nota:
Un número combinatorio o coeficiente binomial, siempre se escribirá como
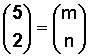
Donde el dígito de arriba será la m (la totalidad de elementos), y el dígito de abajo será la n (los elementos que se toman en cuenta), pero algunos textos o docentes, para indicar que se trata de una combinación, usan la expresión
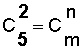
pero siempre la cifra mayor será la m . El alumno siempre deberá usar la fórmula
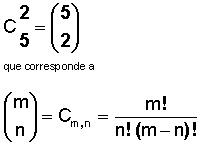
Combinaciones con repetición (CR)
Las combinaciones de m elementos, con repetición, tomados de n en n , son los diferentes grupos de n elementos que se pueden formar a partir de estos m elementos, permitiendo que los elementos se repitan, y considerando que dos grupos se diferencian solamente si tienen elementos diferentes (es decir, no importa el orden). Se representan por CRm,n
Para calcular este tipo de combinación, se usa la fórmula
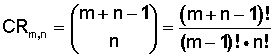
Ejemplo:
Tenemos 5 elementos y queremos saber cuántas combinaciones, con repetición de elementos, se pueden formar tomando solo 3 elementos cada vez.
Veamos:
5 elementos, entonces m = 5
formar grupos de 3 elementos, entonces n = 3 (no entran todos los elementos)
Aplicamos la fórmula con repetición y desarrollamos:
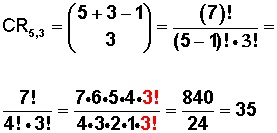
Lo marcado en rojo se ha simplificado.
Combinaciones sin repetición
Las combinaciones de m elementos (la totalidad), sin repetición, tomados de n en n , son los diferentes grupos de elementos que se pueden formar a partir de estos elementos, de modo que dos grupos se diferencian solamente si tienen elementos distintos (es decir, no importa el orden). Se representan por Cm,n .
En este caso, se usa la fórmula
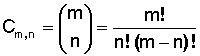
Usando el mismo ejemplo anterior:
Tenemos 5 elementos y queremos saber cuántas combinaciones, sin repetición de elementos, se pueden formar tomando solo 3 elementos cada vez.
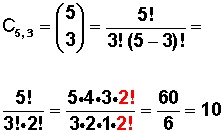
Variación
Si el resultado de una agrupación de elementos considera la inclusión solo de algunos elementos del conjunto, y además importa el orden, estamos hablando de una variación, que puede obtenerse con repetir elementos o sin repetir elementos.
Según esto, podemos tener:
Variaciones sin repetición de elementos
– No entran todos los elementos.
– Sí importa el orden.
– No se repiten los elementos.
Una variación será considerada distinta de otra si difieren en algún elemento o si están situados en distinto orden.
La fórmula que se aplica es:
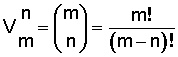
Variaciones con repetición de elementos
Se llaman variaciones, con repetición, de m elementos tomados de n en n a las distintas agrupaciones formados por n elementos de manera que:
– No entran todos los elementos si m es mayor que n. Sí pueden entrar todos los elementos si m = n
– Sí importa el orden.
– Sí se repiten los elementos.
Una variación será considerada distinta de otra si difieren en alguno de los elementos o si están situados en distinto orden.
La fórmula que se aplica es:
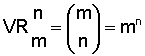
Permutación
Las permutaciones o, también llamadas, ordenaciones, son aquellas formas de agrupar los elementos de un conjunto teniendo en cuenta que:
- Sí importa el orden en que se colocan.
- Se toman todos los elementos de que se dispone.
- Serán Permutaciones sin repetición cuando todos los elementos de que se dispone son distintos.
La fórmula que se utiliza es:
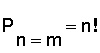
A su vez, serán permutaciones con repetición si disponemos de elementos repetidos.
La fórmula que se utiliza es
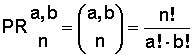
Ir a Ejercicios de Permutaciones
Generalidades sobre Combinatorias
La combinatoria es una sección de las matemáticas que resulta muy útil en variadas disciplinas. Con problemas combinatorios deben enfrentarse los biólogos, físicos, químicos, matemáticos, lingüistas, ingenieros y muchos otros.
El estudio de la combinatoria constituye la base que sostiene el análisis y solución de muchos problemas relacionados con la teoría de las probabilidades y sus aplicaciones prácticas.
Ir a: Probabilidad
Los métodos combinatorios se usan para:
Resolver problemas de transporte
Problemas sobre confección de horarios
Planes de producción y mecanización
Para determinar las características genéticas de razas y animales en laboratorio
Para confeccionar y descifrar claves
Para resolver problemas de la teoría de la información.
En la matemática discreta existen problemas que se resuelven aplicando determinadas fórmulas (según la naturaleza de los elementos combinatorios presentes en ellos) pero la mayoría puede resolverse mediante dos principios generales:
El principio aditivo o regla de la suma y el principio multiplicativo o regla del producto.
Principio aditivo
El número total de combinaciones que se pueden hacer con todas las clases de elementos de un conjunto es igual a la suma de las combinaciones de cada una de las clases.
El principio aditivo permite conocer la composición de todas las muestras de un experimento.
Principio multiplicativo
Si dos cosas pueden ocurrir de manera diferente y una después de la otra, el número total de formas de ocurrencia se obtiene multiplicando el número de formas de la primera con la segunda ocurrencia.
Problemas simples o compuestos
Los problemas combinatorios se clasifican según la cantidad de operaciones que se necesite efectuar para resolverlos en:
Problemas combinatorios simples: que se resuelven mediante una sola operación combinatoria
Problemas combinatorios compuestos: que se resuelven aplicando más de una operación combinatoria.

