Ejercicio 1.

El centro de alumnos del curso necesita nominar un presidente, un vicepresidente y un tesorero para su directiva. ¿De cuántas formas diferentes se pueden cubrir los puestos elegidos de entre los 25 alumnos del curso?

Desarrollo

Primero debemos dilucidar qué tipo de operación combinatoria tenemos.

Para ello, nos hacemos las 3 preguntas básicas:

1.- Para el cálculo, ¿entran todos los elementos?  Respuesta: No, solo entran 3 elementos (3 cargos) de entre 25

2.- En la elección, ¿importa el orden? Respuesta: Sí (jerarquía de cargos)

3.- En el resultado ¿Se repiten los elementos?  Respuesta: No, cada cargo es independiente del otro.

Si revisamos el cuadro anterior (Ver: Mapa conceptual) veremos que se trata de una variación, sin repetición de elementos, que se identifica como:

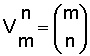
Donde

m = 25

n = 3

Y aplicamos la fórmula:

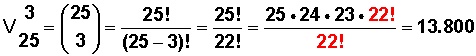
Lo marcado en rojo señala una simplificación (se eliminan), y explicaremos cómo se llega al 22! en el numerador:

Respuesta:

Hay 13.800 opciones de elegir los 3 cargos en el orden requerido.

Ejercicio 2.

¿De cuántas formas pueden mezclarse 8 colores de pintura si las tomamos de 3 en 3?

Desarrollo

Primero debemos dilucidar qué tipo de operación combinatoria tenemos.

Para ello, nos hacemos las 3 preguntas básicas:

1.- Para el cálculo, ¿entran todos los elementos?  Respuesta: No, solo entran 3 elementos (3 colores) de entre 8

2.- En la elección, ¿importa el orden? Respuesta: No

3.- En el resultado ¿Se repiten los elementos?  Respuesta: No, cada color es distinto a otro.

Si revisamos el cuadro anterior (Ver: Mapa conceptual ) veremos que se trata de una combinación, sin repetición de elementos, que se identifica como:

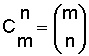
Donde

m = 8

n  = 3

Y aplicamos la fórmula:

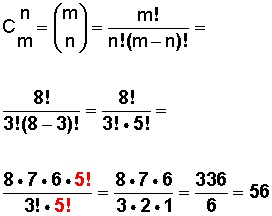
Respuesta:

Si tenemos 8 colores de pintura y los combinamos de 3 en 3, obtendremos 56 combinaciones de colores.

Volver a: Combinatoria