Permutaciones sin elementos repetidos

Las permutaciones sin repetición de n elementos son los distintos grupos que se pueden formar con esos n elementos, de modo que dichos grupos se diferencian entre sí sólo por el orden de colocación de los n elementos.

Como se consideran todos los elementos, y sí importa el orden en que se forman, la fórmula para estas permutaciones sería:

Pn =  n!

Para ene (n) elementos,  igual  ene (n) factorial

Veamos un ejemplo:

Alrededor de una meza hay cinco sillas, ¿de cuántas maneras se pueden ordenar en ellas cinco comensales?

En el ejemplo, n  = 5

Aplicamos la fórmula y queda

Pn =  5!  =  5 * 4 * 3 * 2 * 1 = 120

Los cinco comensales pueden sentarse de 120 maneras distintas en los 5 puestos disponibles. O sea, se pueden obtener 120 permutaciones.

Permutaciones con elementos repetidos

Las permutaciones con repetición de n elementos donde el primer elemento se repite a veces, el segundo b veces, el tercero c veces, ..., son los distintos grupos que pueden formarse con esos n elementos de forma que:

Sí entran todos los elementos

Sí importa el orden

Sí se repiten los elementos

Entonces, el número de elementos (n) está dado por  

 n = a + b + c + ...

Y para calcular el número de permutaciones tomando en cuenta los elementos repetidos, usamos la fórmula siguiente:

Ejercicios de permutaciones con repetición

1.- Calcular las permutaciones con repetición si tenemos 6 bolas amarillas, 4 bolas rojas y 2 bolas verdes.

Nuestra fórmula sería:

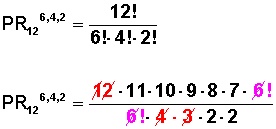
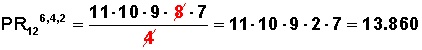
2.- ¿Cuántos números de siete cifras se pueden formar si tenemos 2,2,2,4,4,4,4?

Veamos:

Significa que tenemos 3 números 2, que, para aplicar la fórmula, serían a = 3.

También tenemos 4 números 3, que serían b = 4

Entonces, para conocer n, hacemos   a  + b = 7

Y como

Sí entran todos los elementos

Sí importa el orden

Sí se repiten los elementos

 Aplicamos la fórmula y hacemos las simplificaciones indicadas con color:

Volver a Combinatoria