Movimiento rectilíneo uniformemente acelerado

Ya vimos que el movimiento rectilíneo puede expresarse o presentarse como

Movimiento rectilíneo uniforme ,

o como

Movimiento rectilíneo uniformemente acelerado .

Este último puede, a su vez, presentarse como de caída libre o de subida o tiro vertical .

Un móvil puede ser acelerado.

El movimiento rectilíneo uniformemente acelerado (MRUA) es un tipo de movimiento frecuente en la naturaleza. Una bola que rueda por un plano inclinado o una piedra que cae en el vacío desde lo alto de un edificio son cuerpos que se mueven ganando velocidad con el tiempo de un modo aproximadamente uniforme; es decir, con una aceleración constante.

Este es el significado del movimiento uniformemente acelerado , el cual “en tiempos iguales, adquiere iguales incrementos de rapidez”.

En este tipo de movimiento sobre la partícula u objeto actúa una fuerza que puede ser externa o interna.

En este movimiento la velocidad es variable , nunca permanece constante; lo que si es constante es la aceleración.

Entenderemos como aceleración la variación de la velocidad con respecto al tiempo . Pudiendo ser este cambio en la magnitud (rapidez) , en la dirección o en ambos.

Las variables que entran en juego (con sus respectivas unidades de medida) al estudiar este tipo de movimiento son:

Velocidad inicial           Vo (m/s)

Velocidad final              Vf  (m/s)

Aceleración                     a  (m/s ² )

Tiempo                             t   (s)

Distancia                         d  (m)

Para efectuar  cálculos que permitan resolver problemas usaremos las siguientes fórmulas:

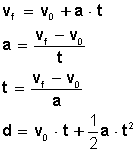
Aunque las anteriores son las ecuaciones principales del movimiento rectilíneo uniformemente acelerado (MRUA) y las únicas necesarias para resolver los ejercicios, en ocasiones resulta útil contar con la siguiente expresión:

Esta fórmula permite relacionar la velocidad con el espacio recorrido y con la "aceleración" y puede ser deducida de las anteriores.

Consejos o datos para resolver problemas:

La primera condición será obtener los valores numéricos de tres de las cinco variables . Definir la ecuación que refleje esas tres variables. Despejar y resolver numéricamente la variable desconocida.

Tener cuidado con que en algunas ocasiones un dato puede venir disfrazado; por ejemplo:

"un móvil que parte del reposo.....", significa que su velocidad inicial es Vo = 0 ; "en una prueba de frenado...", significa que su velocidad final es Vf = 0 .

Veamos un problema como ejemplo

En dirección hacia el sur, un tren viaja inicialmente a 16m/s; si recibe una aceleración constante de 2 m/s ² . ¿Qué tan lejos llegará al cabo de 20 s.? ¿Cuál será su velocidad final en el mismo tiempo?

Veamos los datos que tenemos:

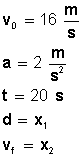
Conocemos tres de las cinco variables, entonces, apliquemos  las  fórmulas:

Averigüemos primero la distancia que recorrerá durante los 20 segundos:

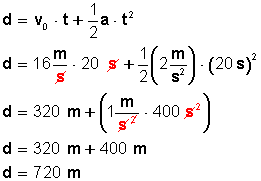
Conozcamos ahora la velocidad final del tren, transcurridos los 20 segundos:

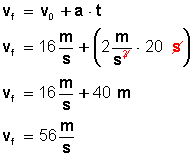
Respuestas:

Si nuestro tren, que viaja a 16 m/s, es acelerado a 2 m/s recorrerá 720 metros durante 20 segundos y alcanzará una velocidad de 56 m/s.

Para practicar, ver el desarrollo de otro ejercicio en:

Ejercicio 01: Movimiento rectilíneo acelerado

Movimiento rectilíneo uniformemente retardado

En los movimientos uniformemente decelerados o retardados la velocidad disminuye con el tiempo a ritmo constante. Están, pues, dotados de una aceleración que aunque negativa es constante. De ahí que todas las fórmulas usadas para los movimientos uniformemente acelerados sirvan para describir los movimientos uniformemente retardados, considerando sólo que su signo es negativo.

Por lo tanto, para efectuar cálculos que permitan resolver problemas que involucren aceleración negativa o deceleración, usaremos las siguientes fórmulas:

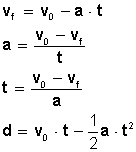
Ir a: Movimiento rectilíneo uniformemente acelerado: Ejercicios01

Ir a Movimiento de caída libre

Ver: Gráficas del movimiento rectilíneo uniformemente acelerado

Ver: Gráficas del movimiento rectilíneo

Fuentes Internet:

http://shibiz.tripod.com/id9.html

http://shibiz.tripod.com/id11.html

http://www.lapaginadejc.com.ar/Naturales/Inicio.htm

http://www.natureduca.com/fis_estumov_movicirc05.php , bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 3.0 Unported