Gráficas del movimiento rectilíneo |
Un modo de describir y estudiar los movimientos es mediante gráficas que representan distancia-tiempo (distancia en función del tiempo), velocidad-tiempo (velocidad en función del tiempo) y aceleración-tiempo (aceleración en función del tiempo).
Debemos anotar que los vocablos distancia, espacio y desplazamiento se usan como sinónimos.
Distancia en función del tiempo
El espacio (distancia o desplazamiento) recorrido en un Movimiento Rectilíneo Uniforme (MRU) puede representarse en función del tiempo. Como en este movimiento el espacio recorrido y el tiempo transcurrido son proporcionales la gráfica es siempre una recta cuya inclinación (pendiente) es el valor de la rapidez (velocidad) del movimiento.
Independientemente del sentido (ascendente o descendente en la gráfica) del movimiento los espacios que recorre el móvil son siempre positivos.
Ecuación de la recta en el Movimiento Rectilíneo Uniforme (MRU)
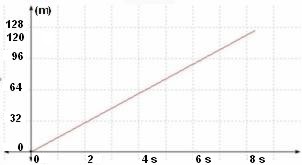
Tenemos el siguiente gráfico:
|
| Gráfica de posición en función del tiempo (posición contra tiempo). |
Los cambios de posición con respecto al tiempo son uniformes
![]()
Dijimos (y así lo vemos arriba) que la gráfica que representa la posición o el espacio recorrido por un móvil en función del tiempo es una línea recta.
También sabemos que la expresión matemática de una recta es:
y = b + mx
Donde:
b es la intersección con el eje vertical.
m es la pendiente de la recta.
La pendiente de la recta (m) se encuentra mediante:
![]()
En nuestro gráfico, entonces, la pendiente es:
![]()
En una gráfica de posición contra tiempo (x - t), la pendiente de la recta me indica la velocidad (V), por lo tanto.
![]()
La ecuación de la recta se encuentra a partir de despejar x de la fórmula para la pendiente
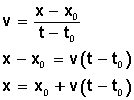
También se la conoce como ecuación del movimiento rectilíneo uniforme (uniforme debido a que la velocidad no cambia, siempre es la misma, es una constante).
Velocidad en función del tiempo
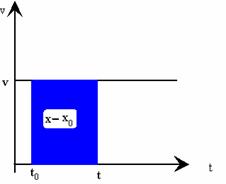
Al realizar la gráfica de velocidad en función del tiempo en el MRU obtenemos una recta paralela al eje X . Podemos calcular el desplazamiento como el área bajo la línea recta.
|
| Gráfica de la velocidad en función del tiempo. |
Otro camino de razonamiento sobre las gráficas en el MRU
Ya aprendimos que un movimiento rectilíneo uniforme es aquel en el que la trayectoria es una línea recta y su velocidad es constante .
La fórmula para conocer la velocidad (rapidez) de un móvil es:
![]()
Entonces, para conocer el espacio recorrido (d) en un MRU basta con despejar d de la expresión de la velocidad:
![]()
Pero también sabemos que en un MRU el espacio recorrido (d) , es igual a la posición final (x) , menos la posición inicial (x 0 ) :
![]()
Si despejamos x, queda
![]()
Entonces, x indica la posición final del móvil, que si la identificamos como (s) , nos queda:
![]()
Ecuación que se corresponde con la ecuación de la recta o ecuación del movimiento rectilíneo : y = b + mx
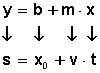
Donde
La incógnita (y) es la posición final del móvil (s)
La intersección en el eje y (b) corresponde al origen del movimiento (x 0 ) o posición inicial.
El valor de la pendiente (m) corresponde al valor de la velocidad del móvil (v) .
Ejemplos para aclarar el tema
Las siguientes gráficas posición-tiempo (posición en función del tiempo) representan dos casos de movimientos rectilíneos uniformes:
1) Gráfica partiendo del origen
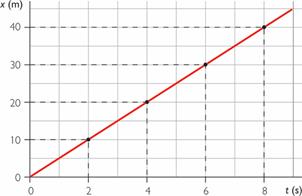
El móvil parte del origen y se aleja de él a una velocidad constante de 5m/s.
La gráfica es una recta ascendente.
Como x 0 = 0 , la posición del móvil, en cada instante, será: x = 5 • t .
2) Gráfica partiendo de un punto situado a cierta distancia del origen
.
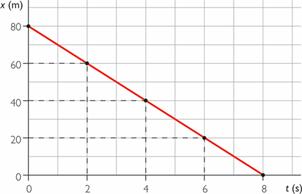
El móvil parte de un punto situado a 80 m del origen y se acerca a él a 10 m/s.
La gráfica es una recta descendente.
Como x 0 = 80 m , la posición, en cada instante, será: x = 80 – 10 • t .
Nótese que 10 (valor de la rapidez) es negativo porque el móvil se está acercando al origen , aunque mantiene su velocidad constante y su aceleración es cero.
| Recuerde que si la pendiente en la gráfica es ascendente, significa que el móvil se aleja del origen, y que si la pendiente es descendente el móvil se acerca al origen. |
Ver: PSU: Física; Pregunta 05_2005(2)
Ejercicio 1)
¿Cuál de los dos movimientos representados tiene mayor velocidad?, ¿por qué?
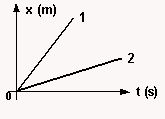
El movimiento 1 es el más rápido (teniendo en cuenta que se comparan en la misma gráfica).
Porque
![]()
Para el caso 1:
![]()
Para el caso 2:
![]()
Para comparar las velocidades debemos igualar los tiempos y consideramos que
![]()
Entonces para un mismo lapso de tiempo (t 2 = t 1 ) notamos que x 1 > x 2 .
Ejercicio 2)
En el gráfico siguiente se representa un movimiento rectilíneo uniforme, averigüe gráfica y analíticamente la distancia recorrida en los primeros 4 s.
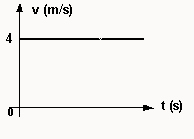
Desarrollo
Datos:
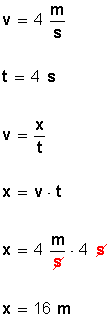
Ejercicio 3)
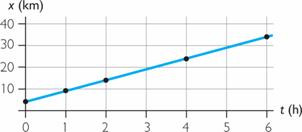
La ecuación del movimiento de una partícula es: x = 4 + 5 · t , donde t está expresado en horas, y x , en kilómetros.
Completamos una tabla x-t y hacemos su representación gráfica.
| Posición (km) |
4 |
9 |
14 |
24 |
34 |
|
Tiempo (h) |
0 |
1 |
2 |
4 |
6 |
Estudiando la gráfica deducimos que se trata de un movimiento rectilíneo uniforme .
Los parámetros de la ecuación son:
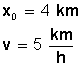
Comprobemos la posición del móvil a las 6 horas:
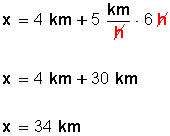
Ejercicio 4)
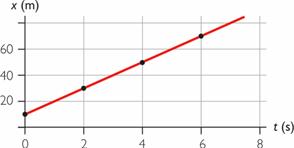
Estudiamos el movimiento de una partícula que se desplaza con MRU a velocidad constante de 10 m/s . La posición inicial de la partícula es x 0 = 10 m .
Los datos nos permiten conformar la siguiente tabla:
|
v (m/s) |
10 |
10 |
10 |
10 |
|
x (m) |
10 |
30 |
50 |
70 |
|
t (s) |
0 |
2 |
4 |
6 |
Gráfica del desplazamiento respecto al tiempo (en función del tiempo)
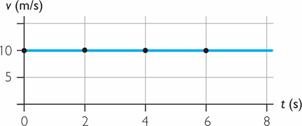
Gráfica de la velocidad respecto al tiempo (en función del tiempo)
Otro ejemplo
:
Un automóvil recorre 70 km cada hora.
Con los datos anteriores se puede elaborar la tabla siguiente:
| punto |
A |
B |
C |
D |
F |
G |
|
distancia (km) |
0 |
70 |
140 |
210 |
280 |
350 |
|
tiempo (h) |
0 |
1 |
2 |
3 |
4 |
5 |
Los datos de esta tabla nos permiten elaborar una gráfica.
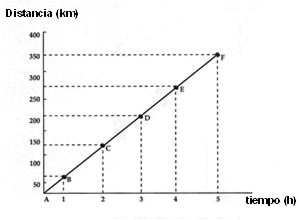
Gráfica de un movimiento rectilíneo uniforme
Se unen con una línea los puntos desde su origen hasta el final.
En la gráfica se observa que al unir los puntos se forma una línea recta, por lo cual se deduce que el movimiento es uniforme, y en este caso el móvil partió del reposo; con ayuda de la gráfica también se puede calcular su velocidad.
Ir a Movimiento rectilíneo uniformemente acelerado
Fuentes Internet:
http://www.educaplus.org/movi/3_2graficas.html
http://newton.cnice.mec.es/materiales_didacticos/mru/rectobjetivos.htm
http://www.fisicanet.com.ar/fisica/cinematica/resueltos/tp01_mru_problema04.php
Ejercicios resueltos en:
http://www.fisicanet.com.ar/fisica/f1_cinematica.php
http://www.pps.k12.or.us/district/depts/edmedia/videoteca/curso2/htmlb/SEC_125.HTM