Movimiento de caída libre

El movimiento de los cuerpos en caída libre (por la acción de su propio peso) es una forma de rectilíneo uniformemente acelerado .

La distancia recorrida (d) se mide sobre la vertical y corresponde, por tanto, a una altura que se representa por la letra h .

En el vacío el movimiento de caída es de aceleración constante, siendo dicha aceleración la misma para todos los cuerpos, independientemente de cuales sean su forma y su peso.

La presencia de aire frena ese movimiento de caída y la aceleración pasa a depender entonces de la forma del cuerpo. No obstante, para cuerpos aproximadamente esféricos, la influencia del medio sobre el movimiento puede despreciarse y tratarse, en una primera aproximación, como si fuera de caída libre.

Torre de experimentación para caída libre de cierta cantidad de átomos, en Bremen, Alemania.

La aceleración en los movimientos de caída libre, conocida como aceleración de la gravedad , se representa por la letra g y toma un valor aproximado de 9,81 m/s2  (algunos usan solo el valor 9,8 o redondean en 10) .

Si el movimiento considerado es de descenso o de caída, el valor de g resulta positivo como corresponde a una auténtica aceleración. Si, por el contrario, es de ascenso en vertical el valor de g se considera negativo, pues se trata, en tal caso, de un movimiento decelerado .

Para resolver problemas con movimiento de caída libre utilizamos las siguientes fórmulas:

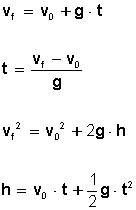
Gota de agua en caída libre.

Algunos datos o consejos para resolver problemas de caída libre:

Recuerda que cuando se informa que “Un objeto se deja caer” la velocidad inicial será siempre igual a cero  (v0 = 0).

En cambio, cuando se informa que “un objeto se lanza” la velocidad inicial será siempre diferente a cero (vo ≠ 0).

Desarrollemos un problema para ejercitarnos

Desde la parte alta de este moderno edificio se deja caer una pelota, si tarda 3 segundos en llegar al piso ¿cuál es la altura del edificio? ¿Con qué velocidad impacta contra el piso?

Desde lo alto dejamos caer una pelota.

Veamos los datos de que disponemos:

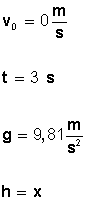
Para conocer la velocidad final (vf) , apliquemos la fórmula

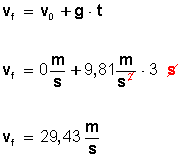
Ahora, para conocer la altura (h) del edificio, aplicamos la fórmula:

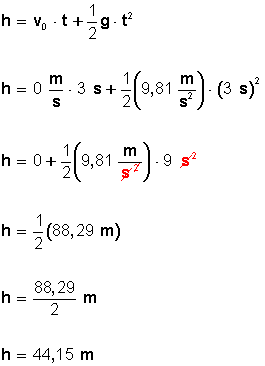
Respuestas :

La pelota se deja caer desde una altura de 44,15 metros e impacta en el suelo con una velocidad de 29,43 metros por segundo.

Ver:

Ejercicio de movimiento con caída libre

Movimiento de subida o de tiro vertical

Al igual que la caída libre, este es un movimiento uniformemente acelerado .

Tal como la caída libre, es un movimiento sujeto a la aceleración de la gravedad (g) , sólo que ahora la aceleración se opone al movimiento inicial del objeto.

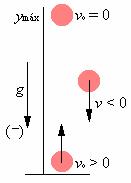
A diferencia de la caída libre, que opera solo de bajada, el tiro vertical comprende subida y bajada de los cuerpos u objetos y posee las siguientes características:

- La velocidad inicial siempre es diferente a cero.

- Mientras el objeto sube, el signo de su velocidad (V) es positivo.

- Su velocidad es cero cuando el objeto  alcanza su altura máxima.

- Cuando comienza a descender, su velocidad será negativa.

- Si el objeto tarda, por ejemplo, 2 s en alcanzar su altura máxima, tardará 2 s en regresar a la posición original, por lo tanto el tiempo que permaneció en el aire el objeto es 4 s.

- Para la misma posición del lanzamiento la velocidad de subida es igual a la velocidad de bajada.

Para resolver problemas con movimiento de subida o tiro vertical  utilizamos las siguientes fórmulas:

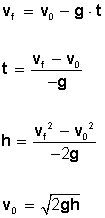
Ver: PSU: Física; Pregunta 10_2005(2)

Para ejercitarnos, resolvamos lo siguiente:

Se lanza verticalmente hacia arriba una pelota con una velocidad inicial de 30 m/s, calcular:

a) Tiempo que tarda en alcanzar su altura máxima.

b) Altura máxima.

c) Posición y velocidad de la pelota a los 2 s de haberse lanzado.

d) Velocidad y posición de la pelota a los 5 s de haber sido lanzada.

e) Tiempo que la pelota estuvo en el aire desde que se lanza hasta que retorna a tierra.

Veamos los datos que tenemos:

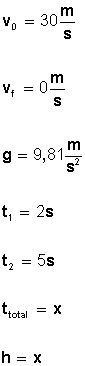
Para conocer el tiempo que demora la pelota en llegar a velocidad cero (altura máxima) utilizamos la fórmula

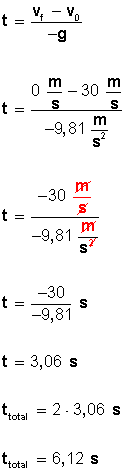
La pelota llega a la altura máxima a los 3,06 segundos y como el tiempo de bajada es igual al de subida, este se multiplica por dos para conocer el tiempo total que permanece en el aire (6,12 segundos).

Ahora vamos a calcular la altura máxima, la que alcanza cuando su velocidad final llega a cero:

Aplicamos la fórmula

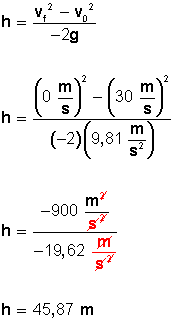
La altura máxima que alcanza la pelota hasta detenerse en el aire es de 45,87 metros (desde allí empieza a caer).

Ahora vamos a calcular la velocidad que tuvo cuando habían transcurrido 2 s:

Aplicamos la fórmula, considerando la velocidad como final a los 2 segundos:

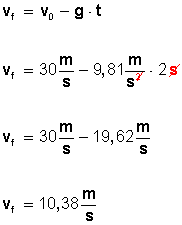
Entonces, la velocidad que llevaba la pelota hacia arriba, a los 2 segundos, fue de 10,38 metros por segundo.

Con este dato, podemos calcular la altura que alcanzó en ese momento (2 segundos).

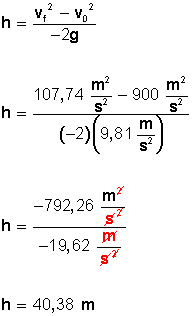
A los 2 segundos la pelota alcanzó una altura de 40,38 metros.

Veamos ahora qué sucede cuando han transcurrido 5 segundos:

Podemos calcular su velocidad usando la misma fórmula

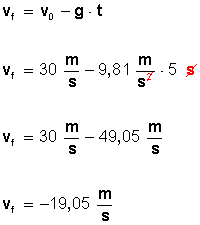
El que obtengamos -19,05 metros por segundo indica que la pelota va cayendo.

También podemos usar la fórmula de caída libre, ya que al llegar a su altura máxima la pelota tiene cero velocidad, pero a los 5 segundos informados debemos restarle los 3,06 segundos durante los que la pelota ha ascendido hasta su altura máxima y desde donde empieza a caer:

Entonces tenemos

5 s – 3,06 s = 1,94 segundo  de caída libre, y su velocidad la dará la fórmula

Pero ahora la velocidad inicial es cero, entonces

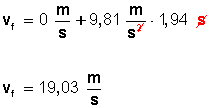
Ahora podemos calcular la altura a que ha llegado la pelota a los 5 segundos; o sea, cuando va cayendo y lleva una velocidad de 19,03 metros por segundo:

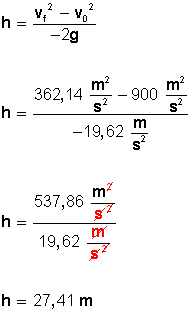
Transcurridos 5 segundos, la pelota va cayendo y se encuentra a 27, 41 metros de altura.

Una pregunta adicional ¿cuánto ha descendido la pelota desde su altura máxima?

Ya sabemos que la altura máxima fue 45,87 metros, entones a esa altura le restamos los 27,41 metros y resulta que la pelota ha descendido 18,46 metros.

Ejercicio de práctica

Resolvamos ahora el siguiente problema:

Un objeto es eyectado verticalmente y alcanza una altura máxima de 45 m desde el nivel de lanzamiento. Considerando la aceleración de gravedad igual a 10 m/s ² y despreciando efectos debidos al roce con el aire, ¿cuánto tiempo duró el ascenso?

Veamos los datos que tenemos:

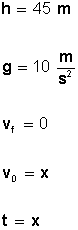
Primero necesitamos calcular (conocer) la velocidad inicial (V0), para ello usamos la fórmula

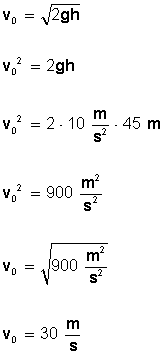
Ahora, para conocer el tiempo que demora el objeto en llegar a velocidad cero (altura máxima = 45 m) utilizamos la fórmula

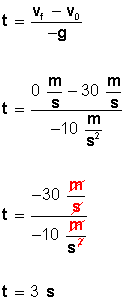
Respuesta: El objeto demora 3 segundos en llegar a 45 metros de altura máxima.

Ver: PSU: Física; Pregunta 13_2005(1)

Ir a: Movimiento rectilíneo uniformemente acelerado

Fuentes Internet:

http://fernandezcanociinthya.blogspot.com/2010_05_01_archive.html

http://www.natureduca.com/fis_estumov_movicirc05.php , bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 3.0 Unported