Al evaluar matemáticamente una función, si conocemos el valor de la variable independiente (x) podemos obtener un valor para la variable dependiente (y). Pero esta misma operación, analizada en el plano del “cálculo infinitesimal”, nos indicaría que ese valor es una referencia, y que representa solo el límite hacia el cual tiende la función, valor al que siempre será posible acercarse, pero sin llegar a él.

El cálculo infinitesimal o simplemente cálculo constituye una parte muy importante de la matemática moderna y se puede definir como el cálculo de una cantidad infinitamente pequeña.

Aquí es conveniente repasar el tema Funciones, en:

https://www.profesorenlinea.cl/matematica/Funciones_matematicas.html

Centrémonos ahora en este nuevo concepto: el límite, que, como vemos, en este apartado adquiere sentido matemático ligado al concepto de función.

Tema aparte será el estudio de límites de las sucesiones.

¿Cómo se llega al límite?

Para entender en simple el concepto de límites, sabemos que entre dos números reales existen infinitos números intermedios.

Tomemos dos números, por ejemplo, 4 y 5, entre ellos está el 4,5  —> 4 .... 4,5 ..... 5

Luego, entre 4 y 4,5 está  4,3       —> 4 ...... 4,3 ..... 4,5

Ahora, entre 4 y 4,3 está 4,1        —> 4 ....... 4,1 ...... 4,3

Luego, entre 4 y 4,1 está 4,08      —> 4 ...... 4,08 .... 4,1

Ahora, entre 4 y 4,08 está 4,001  —> 4 ..... 4,001 .... 4,08.

Y podríamos seguir hasta el infinito colocando decimales entre  el 4 y el 5 y siempre  podremos acercarnos al número "4" todo lo que queramos, sin llegar a él.

En este caso, "4" es el límite que no podemos tocar.

¿Para qué sirve el límite en matemática?

El límite es importante tratándose de funciones, porque en el mundo del “cálculo infinitesimal” es una herramienta fundamental tanto para las matemáticas como para la física.

Cuando se busca el límite, se quiere averiguar a qué valor tiende una función.

El límite debe entenderse siempre como una tendencia: equis (x) sólo se acerca al valor al que tiende, pero nunca puede llegar a ser él mismo.

Por eso, esta herramienta permite comprender el comportamiento de una función o de una sucesión cuando se acerca a un punto dado y sirve para definir conceptos fundamentales como convergencia, continuidad, derivación, entre otros.

En síntesis, el límite es un concepto abstracto fundamental para el estudio del cálculo diferencial e integral.

Uso práctico del límite

Ya vimos que los límites permiten conocer el comportamiento de una función.

En la Antigüedad, desde los tiempos de Grecia, se usaban para calcular áreas.

Hoy en día, los ingenieros usan los límites para conocer los márgenes de seguridad en sus obras.

También la industria, el comercio, la administración utilizan los límites para visualizar resultados.

En general, en muchas áreas de nuestra actividad humana se puede aplicar el límite, lo que resulta muy útil para conocer tendencias y predecir comportamientos.

Expresión matemática del límite de una función

Tomemos como ejemplo la función lineal

f(x) = 2x + 1

que es lo mismo que

y = 2x + 1

Supongamos que se nos pide evaluar la función cuando (x) se aproxima a 3.

Lo cual se escribe así:

El subíndice  x → 3 señala que la función se debe evaluar con valores para x aproximados a 3, pero que no lleguen hasta 3.

Acercarse: por la izquierda y por la derecha

Evaluemos con valores de x menores a 3, pero muy próximos a 3:

¿Qué observamos en las operaciones anteriores?

Los resultados obtenidos para la función son: (6,4), (6,6), (6,8) y (6,98).

¿Qué indica esto? Que cada vez que nos acercamos más a 3, desde un valor más bajo a 3, el resultado de la función se acerca más a 7. (En este caso, se dice que se acerca por la izquierda).

También podemos probar con valores mayores a 3, pero muy próximos a 3:

¿Qué observamos en las operaciones anteriores?

Los resultados obtenidos para la función son: (7,8), (7,6), (7,4) y (7,2).

¿Qué indica esto? Que cada vez que nos acercamos más a 3, desde un valor más alto a 3, el resultado de la función se acerca más a 7. (En este caso, se dice que se acerca por la derecha)

En definitiva, al acercarse a 3 por ambos lados, el límite de la función dada es 7.

El acercarse por la izquierda o hacerlo por la derecha, se denominan límites laterales.

Para indicar que el límite se acerca por la izquierda, se escribe

Y para indicar que el límite se acerca por la derecha, se escribe

Como vemos, en el subíndice x → 3 se agrega un signo menos, si es por la izquierda, y un signo más, si es por la derecha.

Más adelante veremos la relación o la importancia de que el límite sea por la izquierda o por la derecha.

Cálculo por sustitución

En el caso de la función anterior, cuyo valor límite es 7 (valor que conseguimos con varias operaciones), podríamos haber llegado al mismo valor límite 7 en forma directa si reemplazamos la (x) por el valor al que tiende la función (en este ejemplo, ese valor es 3).

De la siguiente manera:

Esta fórmula es la que se aplica generalmente, y vemos que no difiere de cómo se calcula una función cualquiera: Hacemos una sustitución y encontramos un valor final.

Cálculo por factorización

Pero hay casos en que la fórmula de la sustitución no resulta, como en el siguiente ejemplo:

Calcular el límite, cuando x tiende a 1.

Si hacemos la sustitución que vimos anteriormente, esto quedaría así:

Lo cual resulta en una indeterminación matemática, que no tiene existencia.

Una indeterminación matemática es una expresión algebraica que aparece en el cálculo de los límites y cuyo resultado no se puede predecir.

Resulta evidente que con el valor de x = 1 no podemos encontrar un valor para 0/0, pero como sabemos que el valor de x debe aproximarse a 1, podemos probar calculando con valores menores a 1, para acercarnos poco a poco a 1:

En este cuadro, podemos ver que cuando (x) se acerca a 1, (x² — 1)/(x — 1) se acerca a 2.

Pero, ¿si no hacemos el cuadro, o resulta muy engorroso hacerlo?

Entonces podemos utilizar el método de factorización para hacer nuestros cálculos:

Si factorizamos  x² — 1  tendremos  (x + 1) (x — 1), lo que, como producto notable,  se llama una suma por  diferencia, entonces tendremos:

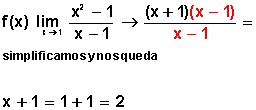
Luego de simplificar (lo indicado en rojo), ahora podemos sustituir el valor de (x) por 1 para obtener el resultado = 2

Cálculo multiplicando por un conjugado

Si el cálculo del límite de una función implica trabajar con fracciones, el límite se resuelve entonces por doble racionalización; es decir, racionalizaremos el numerador y también el denominador. Para racionalizar el denominador, multiplicamos arriba y abajo por su conjugado.

Recordemos que el conjugado de un término es el mismo término, pero con signo contrario.

Por ejemplo:

Conjugado de 4  =  ̶  4

Conjugado de 2x + 1 = 2x  ̶  1

Veamos un ejemplo práctico:

Evaluar el límite para la siguiente función:

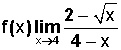
Si la evaluamos con el método de sustitución, y reemplazamos la (x) con 4, el resultado será cero dividido cero (0/0). Lo cual no es válido, es una indeterminación matemática.

¿Qué podemos hacer?

Como tenemos una fracción, podemos racionalizar recurriendo al método del conjugado; en este caso, usaremos el conjugado de arriba (del numerador), y lo multiplicaremos arriba y abajo en la fracción:

El conjugado de

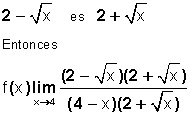
 Ahora, en el numerador encontramos una suma por diferencia (un producto notable), que si recordamos se desarrolla

(a + b) (a - b) = a² – ab + ab - b²  =  a²  –  b²

Según esto, nuestra función nos queda así:

Y ahora podemos sustituir la x con el valor a que tiende la función (4 en este caso):

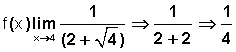
Relación entre límites laterales de una función

En la evaluación de una función normal, el límite de la función en un punto (al que tiende) existe solo si los límites laterales coinciden. Esto ocurre en todas las funciones normales, como en nuestro ejemplo anterior:

Esto significa que cuando  equis (x o punto dado) tiende a 3, el límite siempre será 7, ya sea por la izquierda o por la derecha. Y ese límite sí existe.

Pero los límites laterales (izquierda y derecha) no siempre son iguales.

Esto puede ocurrir, por ejemplo, en las funciones paramétricas, como la siguiente:

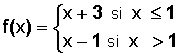
Aquí, la parte superior de la función (x + 3) se evalúa desde la izquierda, con valores iguales o menores a 1.

Y la parte inferior (x – 1) se evalúa desde la derecha, con valores mayores a 1.

Claramente, los límites laterales (izquierda y derecha) no son iguales; por lo tanto, esta función paramétrica no tiene límite en x = 1.

Evaluar límite en funciones polinómicas

Para evaluar el límite de una función polinómica, hay que descomponer en límites individuales cada operación algebraica del polinomio.

Veamos un ejemplo, para evaluar su límite:

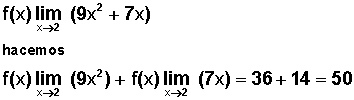
Evaluar límites cuando (x) tiende a cero (0)

Evaluar un límite cuando equis (x) tiende a cero (0) ofrece una buena aproximación para cuando lleguemos al tema de las derivadas.

Veamos el siguiente ejemplo:

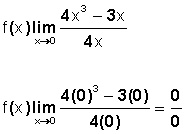
Primero, usamos la sustitución de x por 0, para ver si hay una indeterminación. La cual queda demostrada con el 0/0.

Entonces, debemos utilizar la factorización para evaluar esta función cuyo límite tiende a cero:

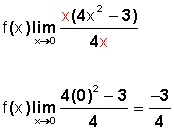
Factorizamos el numerador, sacando la x afuera; luego simplificamos con la x del denominador (lo marcado en rojo) y en seguido sustituimos por cero la x restante.

Ir a: Derivada de una función