En cálculo, derivada es un concepto que tiene varias aplicaciones; pero, fundamentalmente se usa para medir cambios de situaciones límite.

Por ejemplo, una derivada podría señalar la velocidad exacta de un móvil en un punto exacto de su recorrido, si conocemos la velocidad promedio y el espacio total recorrido.

¿Cómo opera la derivada de una función?

La derivada de una función es otra función que evalúa el límite al cual tiende la función original cuando la variable independiente es alterada y su variación tiende al valor cero.

Graficada la función que se evalúa, generalmente mostrando una curva, ese límite (la derivada) señala el valor de la pendiente de una línea que es tangente a la curva en un punto (x₁) determinado. El origen de esta tangente está en una línea secante cuyos puntos x₁ y x₂ están dados por la función original, y la variación que tiende a cero está dada por x₂ – x₁, definida como x + h en la fórmula respectiva.

Esa línea, tangente en cierto punto a la curva que describe una función y cuya pendiente está dada por un valor límite, es la derivada de una función.

Entonces, también podemos decir que la derivada representa el cambio en el valor de la variable dependiente (y) en una función, a medida que su entrada (valor de la variable independiente x) cambia y su variación tiende hacia cero.

El gráfico siguiente explica visualmente lo anterior:

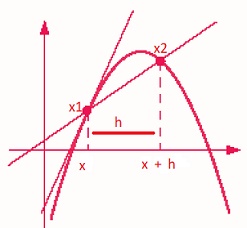
La parábola de la figura es la gráfica de una función en el Plano Cartesiano.

La recta entre x₁ y x₂ es una secante que corta a la parábola

La distancia h es la distancia que debe acercarse a cero; el punto  x + h (x₂) debe acercarse hacia x (x₁).

La recta que pasa por x₁ es la tangente que representa la derivada de la función original y su valor señala la pendiente de la misma.

(Se sugiere ver el tema Recta pendiente)

Aclarados (ojalá entendidos) los conceptos, diremos que la fórmula para calcular una derivada es la siguiente:

En rigor, lo que haremos es formar un numerador restando la función por sí misma:

Con la salvedad de que, para que esa resta tenga sentido, en la primera función reemplazamos cada x por (x  +  h) y queda así:

 
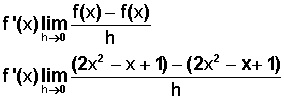
Desarrollemos de inmediato un ejercicio, reemplazando cada x en la primera función por (x + h) y dejando la segunda tal cual la original:

Determinar la función derivada de f(x) = 2x² − x + 1.

 
Como la condición es que la distancia h tienda a cero, sustituimos la h por ese valor y nos queda:

 
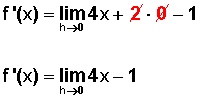
Otra manera de representar la operatividad de una derivada es hacer: diferencial de y sobre diferencial de x.

Para aquellos que ya dominan la operatividad para la obtención de la derivada de una función, la forma sencilla de obtener la derivada es:

El mismo ejemplo anterior: Determinar la función derivada de f(x) = 2x² − x + 1.

Se debe operar cada término:

2x²  = 4x (multiplicar el exponte 2 por el 2 y la x baja un nivel)

̶  x  =  ̶ 1 (recuerden que x es = 1x¹; entonces, multiplican el exponente 1 por el 1 y la x baja un nivel; en este caso, desaparece y queda el 1)

1 = 0  (cualquier valor sin x, desaparece)

Para quedar

f ' (x) = 4x −  1.

Ver: Límite de una función