Razones o relaciones Trigonométricas en el Triángulo Rectángulo |
La trigonometría , enfocada en sus inicios solo al estudio de los triángulos, se utilizó durante siglos en topografía, navegación y astronomía.
Etimológicamente, trigon significa triángulo, y metron , medida. Por lo tanto, trigonometría se puede definirr como "medida de triángulos" .
|
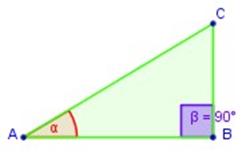
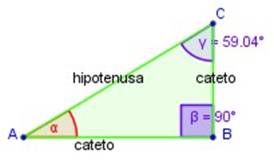
Para establecer las razones trigonométricas, en cualquier triángulo rectángulo, es necesario conocer sus elementos. Para ello, veamos la figura de arriba:
Los ángulos con vértice en A y C son agudos, el ángulo con vértice en B es recto.
Este triángulo se caracteriza por que los lados de los ángulos agudos (α y γ) son la hipotenusa y un cateto, y los lados del ángulo recto (β) son los catetos.
Cada uno de los ángulos águdos del triángulo, uno de cuyos lados es la hipotenusa, se relaciona con los catetos, que pueden ser cateto opuesto al ángulo o cateto adyacente al ángulo.
Cateto adyacente es aquel que forma parte del ángulo al cual se hace referencia.
Cateto opuesto es el lado que no forma parte del ángulo que se toma como referencia y se encuentra enfrente de este.
Con los siguientes ejemplos, veamos lo dicho:
|
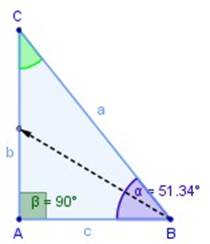
Si consideramos el ángulo α
|
|
|
cateto adyacente
cateto opuesto |
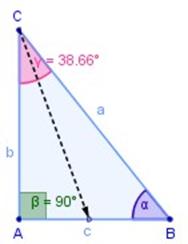
| Si consideramos el ángulo γ |
|
|
cateto adyacente
cateto opuesto |
Por convención, como vemos en los ejemplos, los trazos que son lados del triángulo se pueden representar con las letras mayúsculas correspondientes a sus dos extremos, coronadas con una línea; o bien, con una letra minúscula enfrentando a la correspondiente mayúscula de los ángulos.
Aprendido y recordado lo anterior, veremos ahora que las razones o relaciones trigonométricas se establecen entre dos lados de un triángulo rectángulo en relación con cada uno de sus ángulos agudos. También se llaman Funciones trigonométricas .
Seis son las razones o funciones trigonométricas que se pueden establecer para cualquiera de los dos ángulos agudos en un triángulo rectángulo; de ellas, tres son fundamentales y tres son recíprocas, como lo vemos en el siguiente cuadro:
|
Funciones (razones) trigonométricas
|
|||
|
Fundamentales
|
Recíprocas
|
||
| sen | seno | cosec (csc) | cosecante |
| cos | coseno | sec | secante |
| tan (tg) | tangente | cotan (cotg) | cotangente |
Veamos un ejemplo, para un ángulo α:
|
Sea el ángulo BAC de medida α (siempre menor de 90º) en el triángulo rectángulo ABC .
Los lados BC y BA son los catetos y AC , la hipotenusa. |
En este triángulo rectángulo, las razones trigonométricas con respecto a alfa (α) se definen como:
Seno
![]()
Seno , es la razón (división) entre el cateto opuesto al ángulo y la hipotenusa
Ver: PSU: Geometría;
Coseno
![]()
coseno , es la razón (división) entre el cateto adyacente al ángulo y la hipotenusa
Tangente
![]()
tangente , es la razón entre el cateto opuesto al ángulo y el cateto adyacente al mismo.
Estas tres (seno, coseno, tangente) son las razones fundamentales que se pueden establecer entre un ángulo agudo y los lados del triángulo rectángulo del cual forman parte.
A cada razón fundamental corresponde una razón recíproca , llamadas así por que cada una es la inversa de otra fundamental.
Las tres siguientes son las razones recíprocas que se pueden establecer respecto al mismo ángulo:
Cosecante
![]()
cosecante , es la razón entre la hipotenusa y el cateto opuesto al ángulo, y como es la recíproca del seno de α se puede expresar como
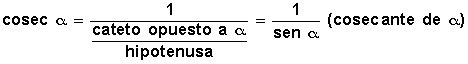
Secante
![]()
secante , es la razón entre la hipotenusa y el cateto adyacente al ángulo, y como es la reciproca del coseno de α se puede expresar como
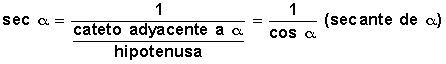
Cotangente
![]()
cotangente , es la razón entre el cateto adyacente al ángulo y el cateto puesto al mismo, y como es la recíproca de la tangente de α se puede expresar como
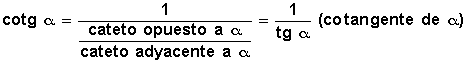
Ahora, hagamos un ejercicio:
|
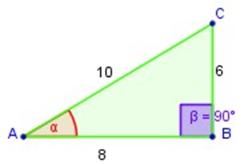
dado el triángulo ABC rectángulo en B (figura arriba).
Sean sus catetos AB = 8 cm y BC = 6 cm .
Aplicamos el Teorema de Pitágoras y calculamos la hipotenusa, que es:
8 2 + 6 2 = 10 2 ; o sea, es igual a 10 cm
entonces podemos calcular las razones trigonométricas:



Ver: PSU: Geometría;
Para Relaciones trigonométricas en triángulos no rectángulos
Ver: Teorema de los senos
Ver: Teorema del coseno
Ir a: Teorema General de Pitágoras
Fuentes Internet:
http://www.pps.k12.or.us/district/depts/edmedia/videoteca/curso3/htmlb/SEC_42.HTM
http://www.luiszegarra.cl/trigo/cap2.pdf