El Teorema del coseno , o Ley de cosenos , es otra generalización del Teorema de Pitágoras utilizado para los triángulos rectángulos, pero que en este caso relaciona un lado de un triángulo cualquiera con los otros dos lados y con el coseno del ángulo formado por esos dos lados:

Sea un triángulo cualquiera con lados a, b y c y con ángulos interiores α, β y γ (son los ángulos opuestos a los lados, respectivamente).

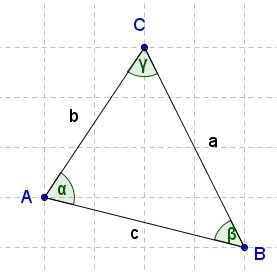
Entonces, se cumplen las relaciones

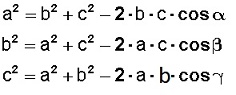
Y el Teorema del coseno se expresa del siguiente modo:

El cuadrado de un lado del triángulo es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de estos dos lados multiplicado por el coseno del ángulo que forman.

Este Teorema del Coseno se usa cuando queremos determinar:

1) el tercer lado de un triángulo si conocemos su ángulo opuesto y los lados adyacentes a este ángulo

2) los ángulos de un triángulo si conocemos los tres lados

Ver: Teorema General de Pitágoras

Hagamos unos ejercicios para aplicar lo dicho hasta ahora.

Problema 1

Se tiene un triángulo cuyos lados a y c miden 45 y 66 cm, respectivamente y cuyo ángulo β mide 47°. Hallar cuánto mide el lado b de este triángulo:

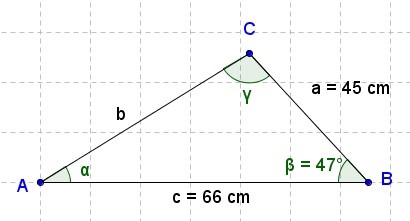
Solución

Para calcular el lado b del triángulo, aplicamos la siguiente fórmula del teorema del coseno:

Como tenemos los datos necesarios, los ponemos en la fórmula y calculamos b:

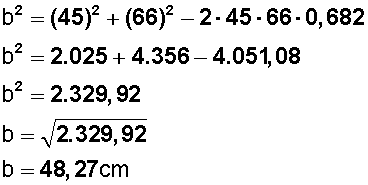
El lado b mide aproximadamente 48,27 cm.

Problema 2

Tenemos el triángulo ABC, donde a = 14 cm, c = 20 cm, y β  = 55°, y nos piden calcular el lado b, y los dos ángulos faltantes, para resolver el triángulo:

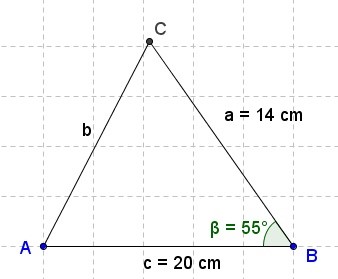
Solución:

Como debemos encontrar b y conocemos su ángulo opuesto (55°), nuestra fórmula será:

b ² = a ² + c ² -2ac cos β

Reemplazamos con los valores conocidos y nos queda:

b ² = (14) ² + (20) ² – 2(14)(20)(0,574)

b ² = 196 + 400 – 321,44

b ² =  274,56

b = √274,56

b = 16,57 cm

Conocidos los tres lados del triángulo, podemos calcular los ángulos faltantes.

Si elegimos calcular el ángulo en A, la ecuación sería:

a ² = b ² + c ² – 2bc cos A

Ponemos el valor de cada lado y despejamos el coseno de A:

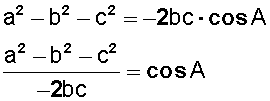
Invertimos la ecuación y queda

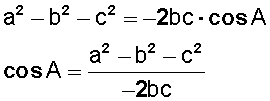
Colocamos los valores que tenemos

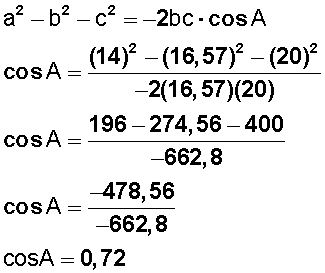
Este es el valor del coseno de A, y conocer el valor del ángulo en grados, aplicamos el coseno inverso:

A = cos ^-1 (0,72) = 43,95 o 43° 57’ 18”

Entonces, el ángulo A, tiene de 43,95 grados o 43° 57’ 18”

Para encontrar el ángulo restante, debemos sumar los ángulos internos del triángulo:

‹ A + ‹ B + ‹ C = 180°

‹ 43,95 + ‹ 55 + ‹ C = 180°

‹ C = 180° - 43,95 – 55

‹ C = 81,05   o  bien 81° 3’

Y tenemos resuelto el triángulo completo

Problema 3

Calcular el valor de los ángulos de un triángulo cuyos lados son a = 12 m,    b = 25 m   y c  = 24 m.

Ejercicio para que lo desarrollen los estudiantes.

Volver a: Teorema de los senos