Pregunta 05_2006

En la figura

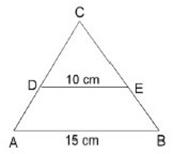
el área del Δ ABC es 90 cm ² y . ¿Cuál es el área del trapecio ADEB ?

Alternativas

A) 36 cm ²

B) 40 cm ²

C) 50 cm ²

D) 54 cm ²

E) 60 cm ²

Contenido: Buscar una estrategia para encontrar el área de la figura pedida .

Comentario:

Para ello debe comprender el enunciado, emplear los datos entregados y aplicar correctamente el Teorema de Thales sobre trazos proporcionales .

Éste dice: “Dos rectas paralelas determinan segmentos proporcionales sobre los lados de un ángulo”.

En la figura trazamos la altura CF

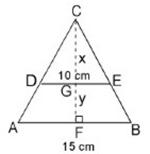
Como y aplicando dicho teorema se tiene que:

, reemplazando se tiene , luego 15x = 10x + 10y , ordenando 5x – 10y = 0 , de donde, dividiendo por 5 queda: x – 2y = 0 (1)

y como área del Δ ABC = 90 cm ² , se tiene , luego 15x + 15y = 180 , de donde x + y = 12 (2)

Luego. formando el sistema de ecuaciones con (1) y con (2), resulta:

Resolviendo este sistema, resulta y = 4 cm , por lo tanto x = 8 cm .

Luego, sabiendo que la altura y del trapecio ADEB es 4 cm, entonces se calcula directamente el área de él como:

Otra forma de determinar el área pedida es calculando la diferencia entre el área del Δ ABC y el Δ DEC, es decir,

Área trapecio ABED = Área Δ ABC – Área Δ DEC .

El área del

Así, el área del trapecio ABED = 90 cm ² – 40 cm ² = 50 cm2 , por lo tanto la clave es C) .

Esta pregunta resultó muy difícil, la contestó bien solamente el 10,2 por ciento de quienes la abordaron y la altísima omisión (65,4 por ciento) demuestra que es un tema desconocido o de muy difícil internalización.

Fuente Internet:

Publicación oficial del Demre en www.demre.cl