Proporcionalidad de trazos en figuras planas |
Proporcionalidad de trazos en triángulos
Se cree que Tales (o Thales) fue uno de los primeros en observar que el paralelismo genera proporcionalidad.
Por ejemplo, si se traza un segmento paralelo a un lado de un triángulo, se genera un nuevo triángulo semejante al original.
Este tipo de trazo (paralelo a un lado del triángulo) es la base para expresar el Teorema particular de Tales , que dice:
Un segmento comprendido entre dos lados de un triángulo y paralelo al tercero, determina sobre éste segmentos proporcionales.
Como corolario, si dos triángulos, ABC y A’B’C’, son semejantes, siempre se pueden analizar bajo los postulados de Tales.
|
Ejemplo:
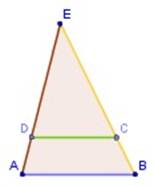
En la figura de la derecha, se tiene que
![]() .
.
Si DC = 8 cm, AB = 12 cm y BC = 3 cm, entonces ¿cuánto mide el trazo CE?
Solución:
Por semejanza de triángulos , tenemos que:
![]()
Según los datos dados y suponiendo que EC = x :
![]() , de lo que se deduce que
x = 6
.
, de lo que se deduce que
x = 6
.
Ver: PSU: Geometría; Pregunta 05_2006
Proporcionalidad de trazos en la circunferencia
En la circunferencia también se pueden presentar situaciones donde se produce proporcionalidad de trazos, las cuales es posible estudiar mediante tres teoremas:
Teorema de las cuerdas
|
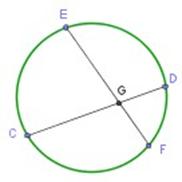
Si dos cuerdas se interceptan en el interior de la circunferencia, el producto de los segmentos determinados en una cuerda es igual al producto de los segmentos determinados en la otra cuerda.
Se cumple que:
EG • GF = CG • GD
Ver: PSU: Geometría;
Teorema de las secantes
|
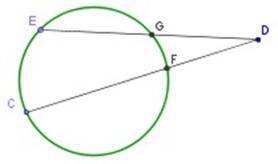
Si dos rectas secantes interceptan a una circunferencia, el producto entre el segmento exterior a la circunferencia con el segmento total en una de las secantes es igual al producto de los correspondientes segmentos en la otra secante.
Se cumple que:
ED • GD = CD • FD
Teorema de la secante y la tangente
|
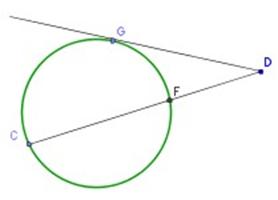
Si desde un punto exterior a una circunferencia, se trazan una tangente y una secante, el cuadrado del segmento tangente equivale al producto entre el segmento exterior y el segmento total de la recta secante.
Se cumple que:
(GD) 2 = CD • FD
Fuentes Internet:
http://geocircuf.blogspot.com/2009/09/teoremas-relacionados-con-la.html

