Pregunta 22_2010

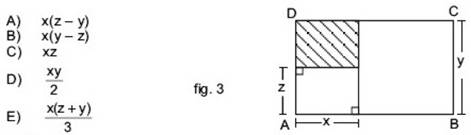
En la figura 3, si ABCD es un rectángulo, entonces el área de la sección achurada se expresa como

Área temática: Álgebra

Comentario

Esta pregunta está relacionada con el contenido del análisis de fórmulas de áreas .

El postulante debe tener la capacidad de comprender el enunciado para luego calcular el área de la región achurada, contenido tratado en Enseñanza Básica.

Como ABCD es un rectángulo y considerando los ángulos rectos marcados en su interior se tiene que la región achurada tiene sus cuatro ángulos interiores rectos; por lo tanto, su área es igual al producto de dos de sus lados contiguos.

Además, BC  =  AD  =  y , con lo cual se concluye que uno de los lados de la región achurada es (y – z) y el otro es x . Luego, el área de esta región es x(y – z) , fórmula que es válida para cualquier medida que tomen sus lados, de esta manera la opción correcta es B) .

La pregunta resultó difícil, lo que demuestra que los alumnos no están habituados a trabajar problemas que relacionen el Álgebra con la Geometría.

El distractor más usado fue C), y el error que seguramente cometen los alumnos es asumir que los dos rectángulos pequeños interiores que se forman en el rectángulo ABCD son congruentes (si lo fueran, estaría indicado en la pregunta), por lo tanto también asumen que los lados del rectángulo achurado son x y z , y así su área es xz .

Fuente Internet:

Publicación oficial del Demre en www.demre.cl