Ecuaciones de la parábola |
Sabemos que la geometría analítica estudia las formas o figuras geométricas basadas en ecuaciones y coordenadas definidas sobre un Plano Cartesiano .
Pues bien, una parábola es una forma geométrica.
Esta forma geométrica, la parábola, expresada como una ecuación , cuenta con una serie de elementos o parámetros que son básicos para su descripción, y son:
Vértice (V) : Punto de la parábola que coincide con el eje focal (llamado también eje de simetría ).
Eje focal (o de simetría) (ef) : Línea recta que divide simétricamente a la parábola en dos brazos y pasa por el vértice.
Foco (F) : Punto fijo de referencia, que no pertenece a la parábola y que se ubica en el eje focal al interior de los brazos de la misma y a una distancia p del vértice.
Directriz (d) : Línea recta perpendicular al eje focal que se ubica a una distancia p del vértice y fuera de los brazos de la parábola.
Distancia focal (p) : Parámetro que indica la magnitud de la distancia entre vértice y foco , así como entre vértice y directriz (ambas distancias son iguales).
Cuerda : Segmento de recta que une dos puntos cualesquiera, pertenecientes a la parábola.
Cuerda focal : Cuerda que pasa por el foco.
Lado recto (LR) : Cuerda focal que es perpendicular al eje focal.
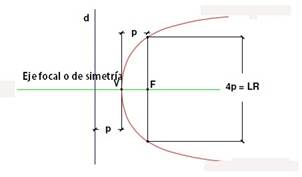
Para ilustrar las definiciones anteriores, veamos la siguiente gráfica de una parábola:
|
En el Plano Cartesiano una parábola puede tener su vértice en cualquier par de coordenadas y puede estar orientada hacia arriba, hacia abajo o hacia la izquierda o la derecha.
Ecuaciones de la parábola con vértice en el origen
Primeramente, estudiaremos la ecuación de la parábola para los casos en que su vértice esté en el origen (coordenadas (0, 0) del Plano Cartesiano) , y según esto, tenemos cuatro posibilidades de ecuación y cada una es característica.
Para iniciar nuestra explicación empezaremos con la parábola cuyo vértice está en el origen, su eje focal o de simetría coincide con el eje de las X (abscisas) y que está orientada (se abre) hacia la derecha.
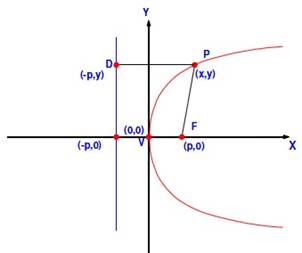
Por definición, sabemos que, en una parábola la distancia entre un punto “P” (no confundir con el “parámetro p” ), cualquiera de coordenadas (x, y), y el foco “F” será igual a la distancia entre la directriz (D) y dicho punto, como vemos en la figura:
|
De lo anterior resulta:
![]() (trazo PD igual al trazo PF)
(trazo PD igual al trazo PF)
El trazo PD nace en el punto (x, y) y termina en el punto (–p, y) y podemos usar la fórmula para calcular distancia entre dos puntos :
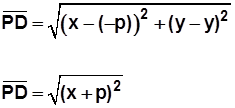
El trazo PF nace en el
punto (x, y)
y termina en el
punto (p, 0)
, y también podemos usar la fórmula para calcular la distancia entre ellos:
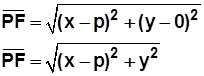
Sustituyendo en la expresión de distancias
![]() resulta:
resulta:
![]()
Elevando ambos miembros de la ecuación al cuadrado y desarrollando, se tiene:
(x + p) 2 = (x – p) 2 + y 2
x 2 + 2px + p 2 = x 2 – 2px + p 2 + y 2
x 2 + 2px + p 2 – x 2 + 2px – p 2 = y 2
Simplificando términos semejantes y reordenando la expresión, se obtiene:
y 2 = 4px |
que es ecuación de la parábola en su forma ordinaria o canónica .
Esta ecuación tiene leves variaciones según sea la orientación de la parábola (hacia donde se abre).
Veamos ahora las cuatro posibilidades:
Primera posibilidad
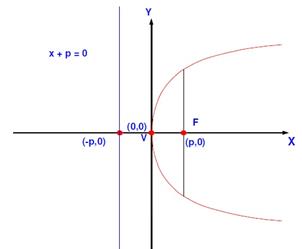
La que ya vimos, cuando la parábola se abre hacia la derecha (sentido positivo) en e l eje de las abscisas “ X”
|
Ecuación de la parábola y 2 = 4px Ecuación de la directriz x + p = 0 |
|
Segunda posibilidad
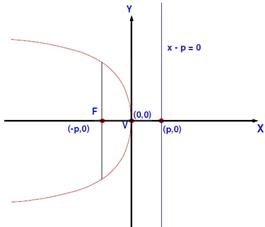
Cuando la parábola se abre hacia la izquierda (sentido negativo) del eje de las abscisas “ X”.
|
Ecuación de la parábola y 2 = 4px (con signo menos final) Ecuación de la directriz x – p = 0 |
|
Tercera posibilidad
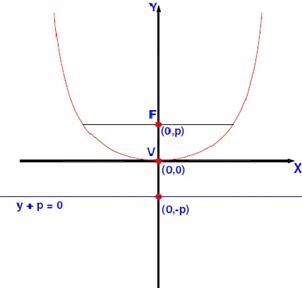
Cuando la parábola se abre hacia arriba (sentido positivo) en el eje de las ordenadas “ Y” .
|
Ecuación de la parábola x 2 = 4py Ecuación de la directriz y + p = 0 |
|
Cuarta posibilidad
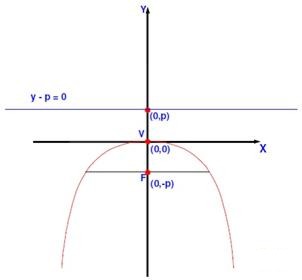
Cuando la parábola se abre hacia abajo (sentido negativo) en el eje de las ordenadas “Y”.
|
Ecuación de la parábola x 2 = 4py (con signo menos final) Ecuación de la directriz y – p = 0 |
|
Información importante:
El parámetro p (que marca la distancia focal) señala la distancia entre el foco y el vértice , que es igual a la distancia entre el vértice y la directriz .
Si en la ecuación de la parábola la incógnita x es la elevada al cuadrado , significa que la curvatura de la misma se abre hacia arriba o hacia abajo, dependiendo del signo del parámetro p .
Cuando el parámetro p es positivo , la parábola se abre “hacia arriba” y cuando es negativo se abre “hacia abajo” .
Ahora, si en la ecuación de la parábola la incógnita y es la elevada al cuadrado , la curvatura de la misma será hacia la derecha o hacia la izquierda. En este caso, cuando el parámetro p es positivo , la parábola se abre “hacia la derecha” y cuando es negativo se abre “hacia la izquierda” .
Longitud del lado recto (LR)
Tal como dedujimos la ecuación anterior, es posible deducir la ecuación que nos permita calcular la longitud del lado recto (cuerda que pasa por el foco, perpendicular al eje focal o de simetría):
No desarrollaremos el camino y sólo diremos, para recordar, que el lado recto es igual a 4p .
Ejemplo:
Obtener la ecuación, el foco y la directriz de la parábola con vértice en el origen y que contiene al punto B(3, 4), además su eje de simetría (o eje focal) es paralelo al eje X.
Resolución:
El punto B (3, 4) nos indica que
X = 3
Y = 4
Sustituyendo las coordenadas del punto B en la ecuación
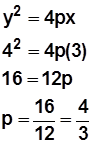
Entonces la ecuación será
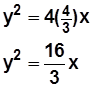
Y el Foco estará en el punto 4/3, 0
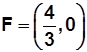
Vemos que 4/3 corresponde al valor de p, y como la directriz está a la misma distancia de p respecto al vértice, pero hacia el lado contrario, entonces, la directriz será:
![]()
Ir a: Ejemplos y Ejercicios
Ir a: Ecuación de la parábola cuyo vértice no está en el origen
Fuentes Internet:
http://dcb.fi-c.unam.mx/cerafin/bancorec/capsulasmatematicas/parabola.pdf
http://matematica1.com/category/conversion-de-la-forma-general-a-la-ordinaria-en-una-parabola/

