Ecuación de la parábola cuyo vértice no está en el origen |
Ahora analizaremos los casos en que se puede obtener la ecuación que describe una parábola cuyo vértice no coincide con el origen del sistema de ejes coordenados.
Cuando el vértice de la parábola se localiza en cualquier punto, por convención ubicado en las coordenadas (h, k) , y distinto al origen, la ecuación que describe a la parábola cambia en función de la posición de este punto y de la orientación de apertura respecto de los ejes x e y .
Debido a estas características, también tenemos cuatro posibilidades de ecuaciones de parábolas cuyo vértice está fuera del origen del sistema de ejes coordenados.
Primera posibilidad
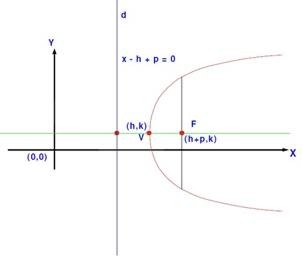
Que la parábola se abra hacia la derecha (sentido positivo) en el eje de las abscisas “X”.
|
Ecuación de la parábola (y – k) 2 = 4p(x – h) Ecuación de la directriz x – h + p = 0 |
|
Segunda posibilidad
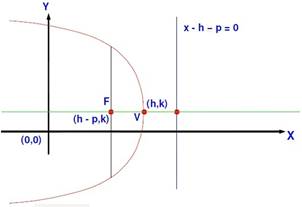
Que la parábola se abra hacia la izquierda (sentido negativo) del eje de las abscisas “ X”.
|
Ecuación de la parábola (y – k) 2 = 4p(x – h) Ecuación de la directriz x – h – p = 0 |
|
Tercera posibilidad
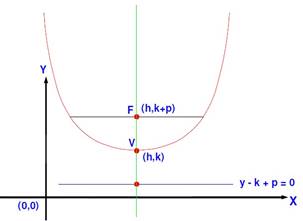
Que la parábola se abra hacia arriba (sentido positivo) del eje de las ordenadas “Y”
|
Ecuación de la parábola (x – h) 2 = 4p(y – k) Ecuación de la directriz y – k + p = 0 |
|
Cuarta posibilidad
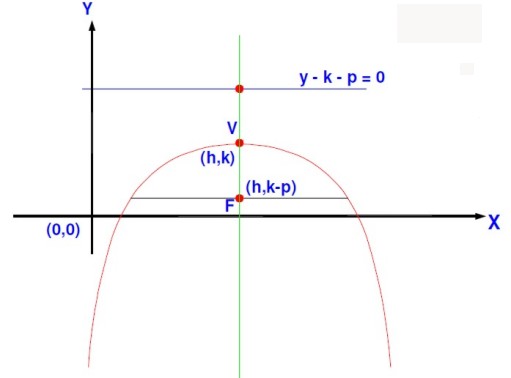
Que la parábola se abra hacia abajo (sentido negativo) del eje de las ordenadas “Y”.
|
Ecuación de la parábola (x – h) 2 = –4p(y – k) Ecuación de la directriz y – k – p = 0 |
|
Recuerde que en todos los casos anteriores la longitud del lado recto siempre será LR = 4p .
Veamos unos ejemplos:
Ejemplo 1:
Encontrar la ecuación de la parábola con vértice en el punto (3, 2) y foco en (5, 2).
Desarrollo
Al analizar las coordenadas de vértice (3, 2) y foco (5, 2), vemos que su ordenada es común (y = 2), por lo que se concluye que están alineados horizontalmente y que el foco está a la derecha del vértice.
Según ya vimos, en este caso la ecuación que resulte tiene la forma
(y – k) 2 = 4p(x – h)
Siendo las coordenadas del vértice (h, k), se sustituyen en la ecuación y resulta:
(y – 2) 2 = 4p(x – 3)
En donde el parámetro p representa la distancia del vértice al foco, que podemos calcular por diferencia de las abscisas correspondientes:
p = 5 – 3
p = 2
Sustituyendo:
(y – 2) 2 = 4(2)(x – 3)
Queda
(y – 2) 2 = 8(x – 3),
ecuación escrita en la forma ordinaria o canónica.
Ejemplo 2
Determine las coordenadas del vértice (V), del foco (F), la longitud del lado recto (LR) y la ecuación de la directriz (D), en una parábola cuya ecuación ordinaria o canónica es (x + 6) 2 = –24(y – 2)
Desarrollo
Estando la x al cuadrado en (x + 6) 2 y siendo negativo el término –24 sabemos de inmediato que la parábola representada en la ecuación es vertical y se abre hacia abajo (sentido negativo de las ordenadas).
Por lo tanto, la forma de dicha ecuación será: (x – h) 2 = –4p(y – k)
Ahora, si las coordenadas del vértice corresponden con los valores de h y k (+6, –2) , y los reemplazamos en la ecuación dada
![]()
Tendremos
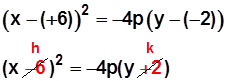
Que nos entrega las coordenadas del vértice
V = (–6, 2)
Además, los datos nos indican que
– 4p = –24
Lo cual significa que la longitud del lado recto (LR) es –24 y por lo tanto
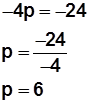
Entonces la distancia focal es 6 (igual a p).
Las coordenadas del foco se obtienen por la abscisa del vértice (–6) y por la diferencia (la resta) entre la ordenada del vértice (2) y la distancia focal (6):
F = (–6, 2 – 6)
F = (–6, –4)
Para determinar ecuación de la directriz se sustituyen los datos conocidos p y k en:
y – k – p = 0
y – 2 – 6 = 0
Resolviendo la ecuación queda:
y – 8 = 0
y = 8
Ir a: Ecuación de la parábola en la forma general

