Multiplicación de un vector por un escalar |
La multiplicación de un vector por un escalar
se puede hacer tanto de manera algebraica como geométrica
.
En ambos casos, el resultado dependerá de si el escalar es positivo mayor que 1; o positivo menor que 1, pero mayor que cero, o si es negativo.
Veamos los casos:
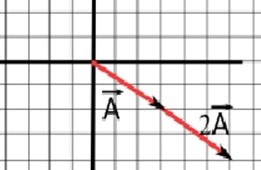
Vector multiplicado por positivo mayor que 1
El vector aumenta de módulo las veces que señala el escalar, y su dirección nunca cambia.
Por ejemplo, tenemos el vector A = (3, –2) y lo multiplicamos por 2:
Modo algebraico:
A = (3, –2) • 2 = A (6, –4)
Modo geométrico:
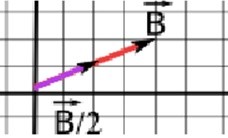
Vector multiplicado por positivo menor que uno y mayor que cero
El vector disminuye un cierto valor, pero mantiene su dirección y sentido.
Por ejemplo, tenemos el vector B = (4, 2) y lo multiplicamos por 0,5.
Modo algebraico:
B = (4, 2) • 0,5 = B = (2, 1)
Modo geométrico:
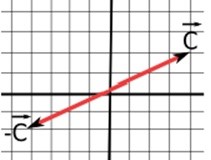
Vector multiplicado por -1 o cualquier número negativo.
Siempre cambiará el sentido del vector resultante, y si el negativo es mayor o menor que 1, cambiará su módulo.
Por ejemplo, tenemos el vector C = (4, 2) multiplicado por –1
Modo algebraico:
C = (4, 2) • –1 = C = (–4, –2)
Modo geométrico:
Volver a: Vectores
Fuentes Internet:
http://definicion.de/vector/#ixzz42Lall9yk
http://definicion.de/vector/#ixzz42Laz71cw
https://www.fisicalab.com/apartado/concepto-de-vector#contenidos
http://es.wikipedia.org/wiki/Vectores

