Sumatoria: Ejercicios de práctica |
Ejercicio 1)
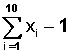 si x = 2 queda
si x = 2 queda
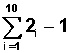
y podemos buscar la secuencia que se repite.
Como sabemos que el límite inferior es 1 y el límite superior es 10, hacemos
(2)(1) – 1 + (2)(2) – 1 + (2)(3) – 1 + (2)(4) – 1 + (2)(5) – 1 + (2)(6) – 1 + (2)(7) – 1 + (2)(8) – 1 + (2)(9) – 1 + (2)(10) – 1
Resolvemos y queda
(2 – 1) + (4 – 1) + (6 – 1) + (8 – 1) + (10 – 1) + (12 – 1) + (14 – 1) + (16 – 1) + (18 – 1) + (20 – 1)
Para finalmente quedar
1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 100
Que resulta ser la suma de los diez primeros impares.
Sabido esto, podemos aplicar la fórmula para sumar n impares consecutivos:
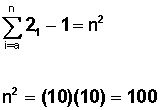
En nuestro ejercicio n = 10
Ejercicio 2)
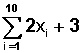 si x = ̶ 5 queda
si x = ̶ 5 queda
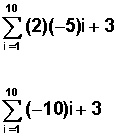
Según las propiedades de la sumatoria, podemos descomponer esta expresión como la sumatoria de sus elementos, de la siguiente manera:
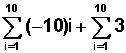
Despejamos la primera sumatoria sacando afuera la constante (k) que es ̶ 10 y cuando esto ocurre (sacar una constante afuera), la fórmula queda así:

Despejamos la segunda sumatoria, cuyos sumandos son solo una constante (3):
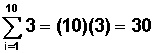
Y sumamos los valores de ambas sumatorias:
– 550 + 30 = – 520
Un camino largo habría sido
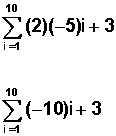
(–10(1) + 3 + (–10(2) + 3 + (–10(3) + 3 + (–10(4) + 3 + (–10(5) + 3 + (–10(6) + 3 + (–10(7) + 3 + (–10(8) + 3 + (–10(9) + 3 + (–10)(10) + 3
Resolviendo
(– 10 + 3) + (– 20 + 3) + (– 30 + 3) + (– 40 + 3) + (– 50 + 3) + (– 60 + 3) + (– 70 + 3) + (– 80 + 3) + (– 90 +3) + (– 100 + 3)
Para finalmente quedar
( – 7) + ( – 17) + ( –27) + ( – 37) + ( – 47) + ( – 57) + ( – 67) + ( – 77) + ( – 87) + ( – 97) =
( – 7 – 17 – 27 – 37 – 47 – 57 – 67 – 77 – 87 – 97 ) = – 520
Ir a Más ejercicios explicativos

