En matemática, representar en forma abreviada la multiplicación de factores iguales se llama potenciación .

En una operación de potenciación, intervienen los siguientes elementos:

a = base

m = exponente

b = la potencia

Lo que en forma generalizada se expresa como

A partir de esta expresión general es posible entender las leyes o reglas de los exponentes.

Primera ley:

Producto de potencias con la igual base.

Para multiplicar potencias con igual base (distinta de cero), se mantiene la base, pero elevada a la suma de los exponentes.

Segunda ley:

Cociente (división) de potencias con la misma base.

Para dividir potencias que tengan la misma base, se mantiene la base, pero  elevada a la diferencia de los exponentes.

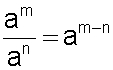
Al respecto, veamos el siguiente ejemplo:

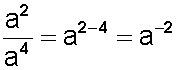
Lo que también se expresa como

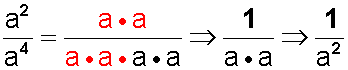
Resultado que por transitividad es igual a:

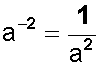
Entonces, podemos concluir que:

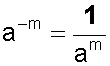
Una base cualquiera elevada a un exponente negativo es igual a su recíproco elevado al mismo exponente, pero positivo.

Tercera ley:

Potencia de una potencia

La potencia de otra potencia con base distinta de cero, es igual a una potencia con esa misma base, pero elevada al producto de los exponentes.

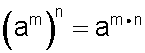
Ver más: Potencia sobre potencia

Cuarta ley:

Potencia de un producto

La potencia de un producto es igual al producto de los factores elevados al exponente común:

Quinta ley:

Un cociente (expresado como fracción) elevado a una potencia, es igual a elevar tanto el numerador como el denominador al mismo exponente.

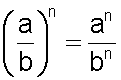
Otros casos

En seguida, tenemos varios casos que pueden deducirse de las leyes ya enunciadas:

1.- División de potencias con igual base e igual exponente.

Si aplicamos le segunda ley, resulta que:

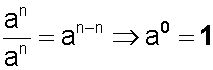
Cualquier base diferente de cero cuyo exponente sea cero, será igual a uno.

2.- Todo número elevado a la primera potencia es igual que ese mismo número

3.- Mención especial merece el caso de la potenciación con exponente fraccionario.

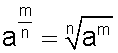
Una base cualquiera elevada a un exponente fraccionario, será igual a extraer raíz de la base elevada al numerador de la fracción, y el grado de la raíz será igual al denominador de la fracción.

Nota final:

Aplicar correctamente estas leyes conduce a obtener los resultados esperados al resolver expresiones algebraicas.

Ver: Cuadro sinóptico con las leyes o reglas (propiedades) de los exponentes

Ir a: Potencias de base entera