Además de ser un número decimal infinito no periódico , los números irracionales tienen otras propiedades como:

Propiedad conmutativa : al sumar o multiplicar números irracionales también se cumple la propiedad conmutativa según la cual el orden de los factores no altera el resultado, por ejemplo, π + ϕ = ϕ + π; así como en la multiplicación, π × ϕ=ϕ × π.

Propiedad asociativa : los números irracionales pueden distribuirse o agruparse de distinta manera entre sí y el resultado  será el mismo. Por ejemplo, en la suma, será  (ϕ + π) +e = ϕ + (π + e); y de la misma manera en la multiplicación, (ϕ × π) × e = ϕ × (π × e).

Propiedad cerrada : es decir que el resultado de la suma o resta de un número irracional, siempre será un número irracional.

En efecto, los números irracionales son cerrados bajo a suma, más no bajo la multiplicación pues la multiplicación de dos irracionales puede ser racional, por ejemplo √2 es irracional y si lo multiplicamos por √8 tendremos √2*√8 = √16 que es 4, un número racional.

Elemento opuesto : existe un inverso aditivo , para la suma de números irracionales; es decir que para cada número existe su negativo que lo anula, por ejemplo π – π=0 y de la misma forma un inverso multiplicativo que da como resultado 1, es decir ϕ × 1/ϕ = 1.

La multiplicación es distributiva en relación a la suma y a la resta. Ejemplo: (3 + 2) π = 3π + 2π = 5π.

Este sí que es famoso: Pi.

Números irracionales famosos

Existen números irracionales determinados que son utilizados en diferentes ramas, para operaciones específicas, algunos de ellos son:

Pi , cuyo símbolo es π, es el más conocido de los números irracionales, y se utiliza en su mayoría para matemáticas, física e ingeniería.

Su valor está dado por el cociente (la división) entre la longitud o perímetro de la circunferencia (como dividendo)  y la longitud de su diámetro (como divisor).

De él se han calculado millones de cifras decimales y hasta ahora no ha sido posible encontrar algún patrón ni menos su término.

La aproximación de su número es 3,141592653589... y por lo general se usa 3,1416.

e es otro número irracional famoso, utilizado en cálculo más que nada, es llamado también número de Euler , y de él también se han calculado infinidad de decimales sin llegar a encontrar una repetición periódica.

Sus primeros decimales son 2,718281828459…

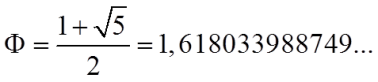
La razón de oro, también conocido como número áureo.

El número áureo o razón de oro , representado con la letra griega ϕ o phi también es muy utilizado por muchos artistas, en especial se lo conoce por las proporciones corporales usadas por Leonardo da Vinci, cuya aproximación es 1,618033988749…

Aparte de los ya mencionados números irracionales, ya habíamos hablado de √2 o raíz cuadrada de 2 que resulta de una ecuación algebraica, pero también están otras raíces.

Volver a: Números irracionales

Fuente Internet:

http://numerosirracionales.com/