Para transformar un número de base decimal a otra base:

Se divide el número por el valor de la nueva base tantas veces como sea necesario hasta obtener un cociente menor que la base; después, se anota como primer dígito este último cociente y se le agregan, desde abajo hacia arriba, los sucesivos restos obtenidos.

Veamos un ejemplo:

Convertir el número 2.034 (base 10) en número base 4

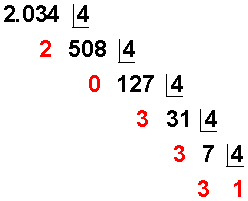
Los números en rojo dan la clave:

Último resultado o cociente = 1  (menor que la base, que es 4) se convierte en el primer dígito del nuevo número.

Luego se agregan los restos de cada división, desde abajo hacia arriba = 33302

Entonces, el nuevo número,  en base 4, es 133302

2.034 ₍₁₀₎ = 133.302 ₍₄₎

Para transformar un número binario (base 2) a un número decimal (base 10):

Se multiplica, partiendo desde la izquierda hacia la derecha,  cada dígito del binario por 2 elevado a la potencia que indique el lugar que ocupa. Dicho lugar se conoce numerando, ahora de derecha a izquierda, desde cero hacia arriba según la cantidad de dígitos que tenga el número binario dado.

Parece enredado explicarlo; por eso, veamos un ejemplo:

Transformar el número binario 10101010111 a otro con base diez.

El número dado tiene 11 (once) dígitos, los cuales se identifican desde 0 (cero) hasta 10 (diez) partiendo desde el último dígito del binario:

Ahora, desde la izquierda hacia la derecha, multiplicamos cada dígito por 2 elevado a la potencia que señala el numerito chico de arriba.

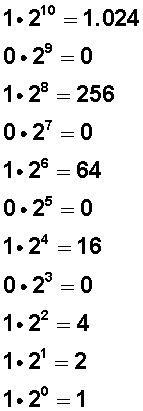
Hacemos la suma de todos los resultados y obtenemos el número en base decimal: 1.367

Respuesta:

El número binario 10101010111 corresponde al número 1.367 en base diez.

Volver a: Bases numéricas