Números: Bases Numéricas |
El sistema numérico que utilizamos actualmente en todos los países es el Sistema de Numeración Decimal . Está formado por diez símbolos llamados dígitos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 . Con estos dígitos, que se pueden combinar, se representan todos los números, los cuales sirven para contar y ordenar.
Ver: http://www.profesorenlinea.cl/matematica/UnidadDecenacentena.htm
Por ejemplo ¿qué significa la representación del número 1.998?

|
Dicho número significa o representa 1 millar (1.000), más 9 centenas (900), más 9 decenas (90), más 8 unidades (8).
En este punto, para aclarar los conceptos, es conveniente recordar las siguientes definiciones:
Sistema Numérico: Se llama sistema numérico al conjunto ordenado de símbolos o dígitos y a las reglas con que se combinan para representar cantidades numéricas.
|
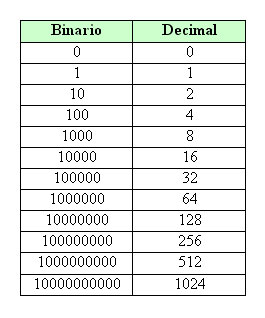
| Un ejemplo de dos bases numéricas. |
Existen diferentes sistemas numéricos , cada uno de ellos se identifica por su base .
Dígito: Un dígito en un sistema numérico es un símbolo que no es combinación de otros y que representa un entero positivo.
Base de un sistema numérico: La base de un sistema numérico es el número de dígitos diferentes usados en ese sistema.
A continuación se ejemplifican estas definiciones con los sistemas numéricos más comúnmente usados que son:
Decimal , utiliza 10 símbolos (dígitos): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Binario , utiliza 2 símbolos (dígitos): 0, 1
Octal , utiliza 8 símbolos (dígitos): 0, 1, 2, 3, 4, 5, 6, 7
Hexadecimal , utiliza 16 símbolos (dígitos): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
U otros con cualquier base:
Terciario (Base 3), utiliza 3 símbolos (dígitos): 0, 1, 2
Cuaternario (Base 4), utiliza 4 símbolos (dígitos): 0, 1, 2, 3
Quinario (Base 5), utiliza 5 símbolos (dígitos): 0, 1, 2, 3, 4

|
Senario (Base 6), utiliza 6 símboloos (dígitos): 0, 1, 2, 3, 4, 5
Heptal (Base 7), utiliza 7 símbolos (dígitos): 0, 1, 2, 3, 4, 5, 6
Nonario (Base 9), utiliza 9 símbolos (dígitos): 0, 1, 2, 3, 4, 5, 6, 7, 8
etc.
Notación: Para distinguir entre los diferentes sistemas numéricos se puede encerrar entre paréntesis el número y se le añade un subíndice que indicará la base que se está usando.
Sin embargo, si no se usa subíndice se deberá entender que el número está en base diez, a menos que se diga lo contrario.
Ejemplos:
35 = (35) 10 = 35 base 10 (sistema decimal)
(110100) 2 = 110100 base 2 (sistema binario)
(453) 4 = 453 base 4

|
También se puede escribir el número sin paréntesis y encerrar el subíndice entre paréntesis:
Ejemplos:
35 = 35 (10) = 35 base 10 (sistema decimal)
110100 (2) = 110100 base 2 (sistema binario)
453 (4) = 453 base 4
Conversión entre sistemas con distinta base numérica
Siempre es posible convertir o transformar los números desde un sistema a otro.
Conversion de binario a decimal
Para transformar números binarios en su correspondiente decimal se multiplica cada dígito binario, que sólo puede ser el 0 (cero) o el 1 (uno), por 2 elevado a la potencia correpondiente a la posición o peso de cada uno. Esta posición o peso de cada dígito se marca desde la derecha a la izquierda, partiendo con el cero, luego uno, dos, tres, cuatro, etcétera, según sea la cantidad de dígitos del número original.
Luego se suman los valores obtenidos y tenemos el número final en base decimal.
Ejemplos:
El número 111 2 (111 en base 2) (binario) corresponde a 7 en base decimal.
Veamos cómo se hace.
Usemos el siguiente cuadro
| Posición o peso (derecha a izquierda) |
|
2 |
1 |
0 |
|
|
|
|
Número binario dado |
|
1 |
1 |
1 |
|
|
|
|
Primer dígito binario (de izquierda a derecha) |
1 x 2 2 |
= |
1 |
x |
4 |
= |
4 |
|
Segundo dígito binario (de izquierda a derecha) |
1 x 2 1 |
= |
1 |
x |
2 |
= |
2 |
|
Tercer dígito binario (de izquierda a derecha) |
1 x 2 0 |
= |
1 |
x |
1 |
= |
1 |
|
Sumamos |
|
|
|
|
|
|
7 |
Otro ejemplo
El número 1101 2 (1101 en base 2) (binario) corresponde a 13 en base decimal.
Veamos cómo se hace.
Usemos el siguiente cuadro
| Posición o peso (derecha a izquierda) |
|
3 |
2 |
1 |
0 |
|
|
|
Número binario dado |
|
1 |
1 |
0 |
1 |
|
|
|
Primer dígito binario (de izquierda a derecha) |
1 x 2 3 |
= |
1 |
x |
8 |
= |
8 |
|
Segundo dígito binario (de izquierda a derecha) |
1 x 2 2 |
= |
1 |
x |
4 |
= |
4 |
|
Tercer dígito binario (de izquierda a derecha) |
0 x 2 1 |
= |
0 |
x |
2 |
= |
0 |
|
Cuarto dígito binario (de izquierda a derecha) |
1 x 2 0 |
= |
1 |
x |
1 |
= |
1 |
|
Sumamos |
|
|
|
|
|
|
13 |
Y para números fraccionarios:
Veamos un ejemplo
El número 0,011 2 (0,011 en base 2) (binario) corresponde a 0,375 en base decimal.
Veamos cómo se hace.
Usemos el siguiente cuadro
| Posición o peso (derecha a izq. |
|
3 |
2 |
1 |
0 |
- 1 |
-2 |
-3 |
|
Número binario |
|
|
|
|
0, |
0 |
1 |
1 |
|
El cero queda tal cual |
|
|
|
|
0, |
|
|
|
|
Primer dígito después de la coma (de izq. a derecha) |
0 x 2 -1 |
= |
0 |
x |
0,5 |
= |
0 |
|
|
Segundo dígito después de la coma (de izq. a derecha) |
1 x 2 -2 |
= |
1 |
x |
0,25 |
= |
0,25 |
|
|
Tercer dígito después de la coma (de izq. a derecha) |
1 x 2 -3 |
= |
1 |
x |
0,125 |
= |
0,125 |
|
|
|
|
|
|
|
|
|
|
|
|
Sumamos |
|
|
|
|
|
|
0,375 |
|
Nota importante:
Podemos convertir números de cualquier base numérica a otro de base decimal usando los mismos cuadros. Solo se cambia la base de la potencia colocando en cada caso como base la base numérica de que se trate.
Veamos un ejemplo:
Convertir el número 1212 (5) (base 5) en número decimal (base 10)
Usemos el mismo cuadro anterior:
| Posición o peso (derecha a izq.) |
|
3 |
2 |
1 |
0 |
|
|
|
Número dado |
|
1 |
2 |
1 |
2 |
|
|
|
Primer dígito (de izq. a derecha) |
1 x 5 3 |
= |
1 |
x |
125 |
= |
125 |
|
Segundo dígito (de izq. a derecha) |
2 x 5 2 |
= |
2 |
x |
25 |
= |
50 |
|
Tercer dígito (de izq. a derecha) |
1 x 5 1 |
= |
1 |
x |
5 |
= |
5 |
|
Cuarto dígito (de izq. a derecha) |
2 x 5 0 |
= |
2 |
x |
1 |
= |
2 |
|
Sumamos |
|
|
|
|
|
|
182 |
1212 (5) = 182 (10) 1212 base 5 corresponde con 182 base 10
Conversión de decimal a binario
Para hacerlo se utiliza el método de divisiones y multiplicaciones sucesivas .
Para convertir un número entero base decimal a una nueva base, el número base decimal es sucesivamente dividido por la nueva base.
Como en nuestro caso la nueva base es 2, el número será sucesivamente dividido por 2,
O sea, el número original es dividido por 2, el resultado de ese cociente es dividido por 2 sucesivamente hasta que el último cociente sea menor a 2.
Los restos de cada división, ordenados desde abajo hacia arriba, se agregan para conforman el número binario buscado.
Entonces, tomamos el último cociente y los restos hacia arriba, para formar el número binario resultante de la conversión.
Veamos esto con un ejemplo:
Convertiremos a binario el número 18 10 (base 10) sistema decimal
| 18 : |
2 |
|
|
|
18 dividido 2 |
|
0 |
9 : |
2 |
|
|
9 dividido 2 |
|
|
1 |
4 : |
2 |
|
4 dividido 2 |
|
|
|
0 |
2 : |
2 |
2 dividido 2 |
|
|
|
|
0 |
1 |
es el primer dígito del binario |
Desde el 1 (primer dígito del binario) anotamos los restos de las divisiones previas, hacia arriba:
Estos restos son: 0, 0, 1, 0, los cuales escribimos a continuación del 1 (primer dígito del binario):
1 0 0 1 0 y tenemos el número binario que corresponde al 18 decimal
1 0 0 1 0 (2) binario = 18 (10) decimal

|
Convertir un decimal fraccionario a binario
En el caso de convertir a binario un número decimal fraccionario , la parte fraccionaria (lo que está después de la coma) debe ser multiplicada por 2 y el número binario será formado por los ceros (0) o unos (1) que aparecen en la parte correspondiente al entero en cada multiplicación.
Solo que en este caso el número binario se escribe de izquierda a derecha, a diferencia de lo explicado antes para los números enteros.
Las multiplicaciones se efectúan solo sobre la parte fraccionaria del número por lo que siempre serán 0,XXX.
Nunca debe multiplicar 1,XXX.
El proceso de multiplicaciones sucesivas concluye cuando quedan en cero la parte entera y la fraccionaria.
En este ejemplo convertiremos el número decimal fraccionario 0,625 (10)
0,625 x 2 = 1, 250 (lo que está después de la coma: 250) lo multiplicamos por 2
0,250 x 2 = 0, 500 (lo que está después de la coma:500) lo multiplicamos por 2
0,500 x 2 = 1, 000 (lo que está después de la coma: 000) marca el final de la operación.
La operación concluye porque no queda parte fraccionaria para seguir multiplicando.
Entonces:
0,625 (10) = 0,101 (2)
Conversión de decimal a número con otra base
En esos casos basta usar el mismo método de conversión de decimal a números binarios. Pero en vez de hacer divisiones sucesivas por 2 hay que efectuarlas por el número que indica la nueva base.
Veamos el siguiente ejemplo:
Convertir el número 144 (10) en número base 7
| 144 : |
7 |
|
|
|
144 dividido 7 |
|
4 |
20 : |
7 |
|
|
20 dividido 7 |
|
|
6 |
2 |
|
|
es el primer dígito del número nuevo |
Entonces:
Desde el 2 (primer dígito del número nuevo) anotamos los restos hacia arriba: 2 6 4
264 (7) = 144 (10) 264 base 7 corresponde a 144 base 10
Ir a: Bases numéricas: Ejercicios
Fuentes Internet:
http://www.pablin.com.ar/computer/cursos/varios/basesnum.htm
http://lc.fie.umich.mx/~jrincon/elec3-cap1.pdf
Una buena calculadora para converir base numérica en:
http://miayudante.upn.mx/html/basebase.html

