Tipos de matrices

Estudiado y comprendido el concepto de matriz , y conocidos todos sus elementos, podemos agregar que existen ciertas matrices que aparecen frecuentemente y que reciben nombres característicos.

Veamos cuáles son:

Matriz fila

Como su nombre lo dice, es una matriz que solo tiene una fila; es decir, m = 1 y por tanto es de orden 1 x n .

Ejemplo

Matriz columna

De nuevo, su nombre lo indica: Es una matriz que solo tiene una columna; es decir, n = 1 y por tanto es de orden m ´ 1.

Ejemplo

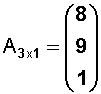
Matriz nula

Fiel a su nombre,  es aquella matriz en que todos sus elementos son 0 (cero)  y se representa por 0 (cero) .

Ejemplo

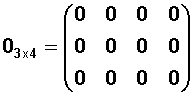
Matriz cuadrada

Es aquella que tiene el mismo número de filas que de columnas; es decir, m = n. En estos casos se dice que la matriz cuadrada es de orden n, y no n ´ n.

Ejemplo

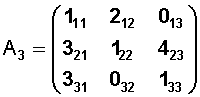
En este ejemplo hemos identificado cada elemento en su correspondiente fila y columna.

Esto para mostrar que aquellos elementos donde i = j (que  son 1 ₁₁ , 1 ₂₂ y 1 ₃₃ ) forman la llamada diagonal principal de la matriz cuadrada .

A su vez, aquellos elementos donde i + j = n + 1 (que son 0 ₁₃ , 1 ₂₂ y 3 ₃₁ ) forman la diagonal secundaria (en este ejemplo, n + 1 = 4 , ya que n es igual a 3 , valor que representa el número de filas que tiene la matriz).

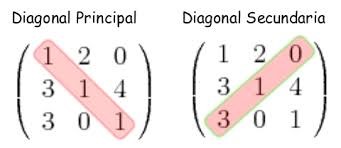
Entonces, vemos que la diagonal principal está formada por (1, 1, 1) y la diagonal secundaria por (0, 1, 3).

Matriz traspuesta

Si tenemos una matriz A , y a esta le cambiamos sus filas por columnas tendremos una matriz traspuesta de A y que se representa por A ^t .

La primera columna de At, la formamos con la primera fila de A; la segunda columna de At, la formamos con la segunda fila de A, y así, sucesivamente.

De la definición se deduce que si

A es de orden m x n, entonces A ^t es de orden n x m

Si tenemos que

A = (a _ij ) _{m x n}

entonces su matriz traspuesta será

A ^t = (a _ij ) _{n x m}

Ejemplo

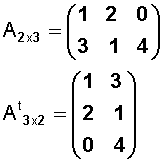
Matriz diagonal

Es una matriz cuadrada, en la que todos los elementos no pertenecientes a la diagonal principal son nulos.

Ejemplo

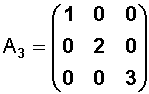
Matriz simétrica

Una matriz cuadrada A es simétrica si A = A ^t .

Ejemplo

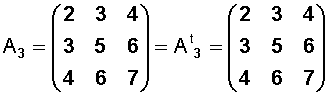
Matriz escalar

Es una matriz diagonal con todos los elementos de la diagonal principal iguales.

Ejemplo

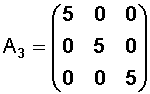
Matriz identidad

Es una matriz escalar con los elementos de la diagonal principal iguales a 1, y se representa por I .

Ejemplo

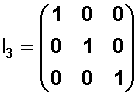
Ir a:

Operaciones con matrices y sus propiedades

Concepto de matriz