Concepto de matriz |
En matemática, se denomina matriz a todo conjunto de números o expresiones que aparecen distribuidos ordenadamente en forma rectangular, formando filas y columnas .
De modo general, estas filas y columnas se identifican con las letras m y n. La m para las filas y la n para las columnas.
Cada uno de los números de que consta la matriz se denomina elemento . Un elemento se distingue de otro por la posición que ocupa; es decir, la fila y la columna a las que pertenece.

|
| Distribución ordenada en forma rectangular, formando filas y columnas: una matriz. |
El número de elementos de una matriz lo obtendremos de multiplicar el número de filas por el de columnas: m x n (m por n) .
La expresión de este producto (m x n) indica a su vez el orden de matriz (o dimensión de una matriz o tamaño de una matriz) .
Cuando decimos que una matriz es de orden o dimensión 3 x 4 estamos diciendo que se trata de una matriz de 3 filas y 4 columnas.
En general, el conjunto de matrices de m filas y n columnas se denota por
A mxn
En el ejemplo anterior, tendríamos una matriz
A 3x4
Y un elemento cualquiera de la misma, que se encuentra en la fila i y en la columna j , se denotará por
a ij
En nuestro ejemplo, el primer subíndice, “i”, indica la fila (con su correspondiente número) a la que pertenece el elemento y el segundo subíndice, “j”, representa la columna también con su correspondiente número.
Ejemplo: un elemento que esté en la fila 2 columna 3 será
a 23
Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan el mismo lugar en ambas son iguales.
Como ya lo hemos visto en los ejemplos, las matrices se representan por letras mayúsculas A, B, C...
Y, reiteramos, a los números a ij se les denomina elementos de la matriz.
Tratemos de visualizar lo dicho anteriormente:
Una matriz de orden o dimensión m x n es una disposición de números ordenados en m filas y n columnas de la forma
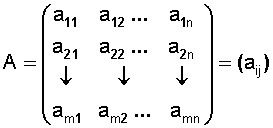
Veamos algunos ejemplos numéricos:
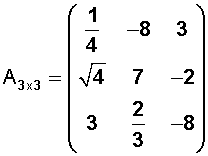
En este ejemplo la fila 1 es
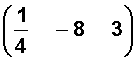
La fila 2 es
![]()
La fila 3 es
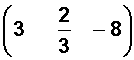
La columna 1 es
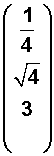
La columna 2 es

La columna 3 es

Ir a:
Tipos de matrices

