División sintética o regla de Ruffini |
A continuación, veremos cómo realizar la división de un polinomio por un binomio usando la
división sintética o regla de Ruffini
.
Para explicar este procedimiento, veamos un ejemplo:
6x 3 – 2x dividido entre 4x + 8
Para realizar una división sintética deben cumplirse las siguientes condiciones:
1) Tanto dividendo (6x 3 – 2x) como divisor (4x + 8) deben tener la misma letra (en este caso la x)
2) El polinomio divisor (4x + 8) debe ser de primer grado (la equis elevada a uno).
3) Los términos del polinomio dividendo (6x 3 – 2x) deben estar agrupados de mayor a menor según su exponente (x4, x3, x2, x, 4 por ejemplo).
4) El polinomio dividendo (6x 3 – 2x) debe estar completo según sea el exponente mayor (en este ejemplo faltarían x 2 y la cifra final).
5) Si el polinomio dividendo (6x 3 – 2x) no está completo debe completarse con ceros.
En nuestro caso, el polinomio dividendo (6x 3 – 2x) debe quedar como 6x 3 + 0x 2 – 2x + 0 para empezar a operar.
Y hacemos lo siguiente:
El polinomio divisor (4x + 8) lo igualamos a cero y despejamos la x
4x + 8 = 0
4x = – 8
x = –8/4
x = –2
Luego hacemos un cuadro como sigue, anotando debajo de cada término solo su coeficiente, colocando el valor de x ( – 2) en la línea siguiente y repitiendo abajo el primer coeficiente (6 en color rojo):
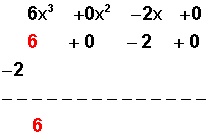
En seguida, este primer coeficiente (6) lo multiplicamos por el valor de x (– 2), lo cual da – 12.
Este –12 lo ponemos bajo el siguiente coeficiente ( + 0) y sumamos la columna ( + 0 + –12 = – 12), así (indicado en rojo):
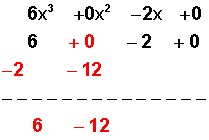
Y continuamos:
El –12 lo multiplicamos ahora por –2, nos da +24 y lo ponemos bajo el siguiente coeficiente (–2), y sumamos la columna (–2 + 24 = +22).
Y repetimos: ahora el +22 lo multiplicamos por –2 y nos da – 44, que ponemos bajo el siguiente coeficiente (+ 0) y sumamos la columna (–0 + –44 = –44)
El cuadro completo queda así:
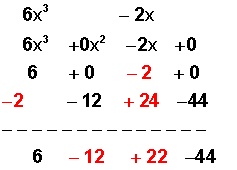
Ahora agregamos la incógnita a cada término, sabiendo que en cada columna disminuye un grado:
![]()
Aquí, establecemos que –44 es el residuo; pero, en este punto debemos fijarnos en el coeficiente que tiene la x de nuestro divisor (4x + 8).
Este coeficiente de la x es 4; por lo tanto, en el resultado anterior debemos dividir cada término entre 4 (exceptuando el residuo), para quedar:
![]()
Expresión que, simplificando, reducimos a:
![]()
Entonces, –44 es el residuo y
![]()
Es el cociente de la división sintética.
Ejercicio 1)
Dividir
![]()
Hacemos
x – 2 = 0
x = 2
Luego, el cuadro
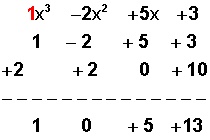
Donde 13 es el residuo y el cociente es
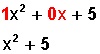
Nótese que lo marcado en rojo no se escribe.

