Cilindro: área y volumen |
Un cilindro circular recto es aquel cuerpo o sólido geométrico generado por el giro de una región rectangular en torno a uno de sus lados o también en torno a uno de sus ejes de simetría.
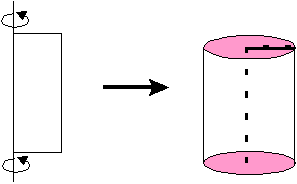
El cilindro
consta de dos bases circulares y una superficie lateral que, al desarrollarse,
da lugar a un rectángulo. La distancia entre las bases es la altura del
cilindro. Las rectas contenidas en la superficie lateral, perpendiculares a las
bases, se llaman generatrices.
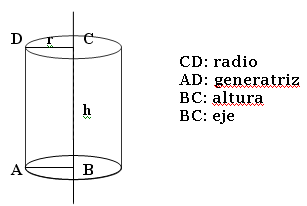
Si “abrimos” un cilindro recto a lo largo de una generatriz, y lo extendemos en un plano, obtenemos dos círculos y una región rectangular. De esta manera se obtiene la red del cilindro recto.
Para desarrollar o dibujar un cilindro, ver figura:
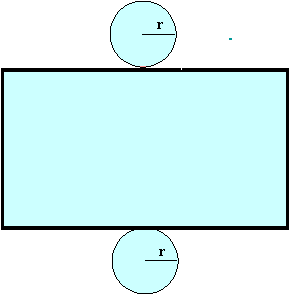
Perímetro: es la línea que limita una figura plana.
Área lateral: Superficie de un cuerpo geométrico excluyendo las bases.
Área total: Superficie completa de la figura, es decir, el área lateral más el área de las bases de la figura.
Área del cilindro
El área lateral del cilindro está determinada por el área de la región rectangular, cuyo largo corresponde al perímetro de su base, es decir a 2 Π r , y cuyo ancho es la medida de la altura del cilindro, o sea h .
Para calcular su área lateral se emplea la siguiente fórmula:
|
Área lateral = perímetro
de la base x altura
|
|
A lateral = 2 π r . h
|
Si a la expresión anterior le sumamos el área de las dos regiones circulares basales, obtenemos el área total del cilindro.
Para calcular su área total se emplea la siguiente fórmula:
|
Área
total = área lateral + 2 x área de la base
|
|
A
total
= A
lateral
+ 2A
base
|
Entonces,
A total = 2 Π r h + 2 Π r 2
Por lo tanto:
A total = 2 Π r ( h + r )
Volumen del cilindro
Para un cilindro circular, su volumen (V) es igual al producto del área del círculo basal por su altura (h).
Para calcular su volumen se emplea la siguiente fórmula:
|
Volumen del cilindro =
área de la base x altura
|
|
|
Es
decir,
|
V cilindro = A base · h |
| V cilindro = Π r 2 · h | |
Ejemplo:
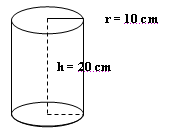
|
¿Cuál es el área total de un cilindro si su radio basal mide 10 cm y su altura mide 20 cm?
Se sabe que: r = 10 cm y h = 20 cm
2 Π · 10 cm (20 cm + 10 cm) = 20 Π cm (30 cm) = 600 Π cm 2
A total = 600 Π cm 2 = 600 x 3,14 = 1.884 cm 2
¿Cuál es el volumen del cilindro anterior?
Se sabe que: r = 10 cm y h = 20 cm
Π (10 cm) 2 · 20 cm = 2000 Π cm 3 = 6.283 cm 3
V cilindro = 6.283 cm 3
Para practicar esta materia, ir a:
Volumen de un cilindro, Ejercicio 1
Volumen de un cilindro, Ejercicio 2

