Ejercicio 1)

El desarrollo de la superficie lateral de un cilindro recto extiende un cuadrado de área S, que se ve en la figura de abajo. Calcular el volumen de dicho cilindro.

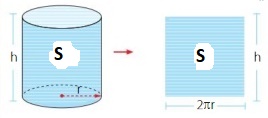
Solución:

Sabemos que un lado del cuadrado corresponde al perímetro de la circunferencia que da origen a la base del cilindro:

El perímetro de una circunferencia está dado por la fórmula 2πr.

Ver el tema en:

https://www.profesorenlinea.cl/geometria/circulocircunferencia.htm

Como el desarrollo del cilindro indica que es un cuadrado, entonces

Tenemos 2πr *  h   =  S    (base por altura)

Ver, Área del cuadrado en:

https://www.profesorenlinea.cl/geometria/PerimetroArea.htm

Pero, en nuestro caso

2πr =  h  ( por que es un cuadrado)

Y por lo tanto h²  = S, por ende  (extrayendo raíz a ambos lados) queda

 
Como consecuencia

 
 y de aquí podemos calcular r (valor del radio)

 
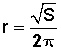
Conocido el radio, podemos calcular el volumen, que está dado por la fórmula

 
Reemplazamos los valores y queda

 
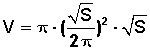
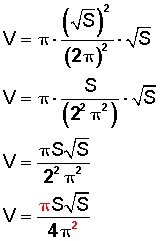
Simplificamos (eliminamos términos comunes, en rojo) y queda

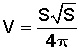
Ir a Ejercicio 2)