Semejanza de figuras planas |
El concepto de semejanza en la vida cotidiana
En lenguaje cotidiano, cuando se habla de semejanza , casi siempre se hace referencia al concepto más general de parecido : color “parecido”, tamaño “parecido”, forma “parecida”, etcétera.
En los ejemplos, el significado de semejanza que hacemos notar hace referencia a una característica común entre objetos o personas: color, tamaño y forma, entre otros.
El concepto de semejanza en matemática
En cambio, en matemática el concepto de semejanza está muy ligado al concepto de proporcionalidad ; por ello se dice que dos objetos son semejantes si "tienen" una proporción entre ellos.
Por ejemplo, un mapa es una representación semejante a una porción del globo terráqueo, de allí que deba tener una misma proporción, para que las medidas que se tomen sobre él sean lo más cercanas a su valor real.
Ahora, si tenemos dos anillos idénticos, cuyos diámetros son exactamente iguales, diremos que tienen la misma proporción y semejanza entre cada una de sus partes (circunferencia, radio, área, diámetro).
Ver: Proporcionalidad de trazos en figuras planas y
Ver: Congruencia de triángulos
En Geometría, diremos que dos figuras son semejantes ( ~ es el signo de semejanza) si, y solo si, tienen la misma forma pero no necesariamente el mismo tamaño; para mayor comprensión, podrìamos decir que una figura corresponde a una "ampliación" de la otra.
Consideraciones importantes:
Si dos polígonos regulares tienen igual número de lados, entonces son semejantes.
Toda circunferencia es semejante a otra circunferencia.
La congruencia es un caso particular de la semejanza.
Semejanza de triángulos
En el estudio de la semejanza entre figuras planas , el tópico de la semejanza de triángulos es muy importante para quienes postulen a la PSU .
De modo general, diremos que dos triángulos son semejantes cuando los ángulos de uno de ellos sean respectivamente congruentes con los ángulos del otro y, además, tengan proporcionales sus lados homólogos (correspondientes).
Para avanzar en la comprensión del concepto de semejanza es preciso definir y entender qué son lados homólogos (correspondientes) y qué es proporcionalidad .
Tenemos la figura siguiente:
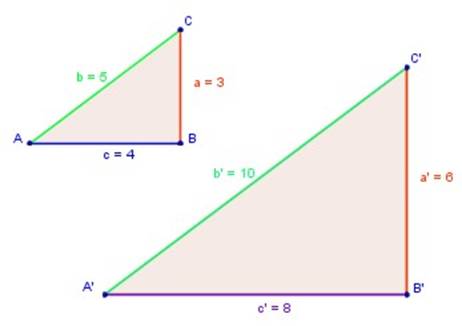
Veamos:
Los lados homólogos (correspondientes) son, respectivamente:
a y a' (de color rojo, lado pequeño y lado pequeño)
b y b' (de color verde, lado grande y lado grande)
c y c' (de color azul, lado mediano y lado mediano)
Si hacemos la división entre los lados homólogos (correspondientes) el resultado es 2 (10 dividido5, 8 dividido 4 y 6 dividido 3); este valor recibe el nombre de razón y cuando la razón es igual en todos y cada uno de los lados homólogos (correspondientes), se dice que los lados son proporcionales.
Para comprobar si dos triángulos son semejantes existen teoremas o criterios de semejanza , los cuales ayudan a determinar la semejanza o no de dos triángulos.
Importante
Cuando se dice que el triángulo ABC es semejante con el triángulo DEF, se escribe:
Δ ABC ~ Δ DEF
Es muy importante el orden en que se escriban los vértices de cada triángulo, ya que esto establece los lados y los ángulos homólogos.
En el ejemplo anterior, se tiene que:
El vértice A es homólogo con el vértice D
El vértice B es homólogo con el vértice E
El vértice C es homólogo con el vértice F
El lado AB es homólogo con el lado DE
El lado BC es homólogo con el lado EF
El lado AC es homólogo con el lado DF
Ahora podemos postular el que se considera como Teorema Fundamental de la Semejanza de Triángulos :
Toda paralela a cualquier lado de un triángulo forma con los otros dos lados un triángulo semejante al primero, y para que dos triángulos sean semejantes basta con que cada uno posea dos ángulos congruentes.
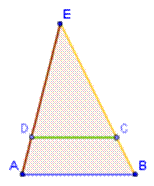
|
Si trasladamos el concepto hacia la imagen de arriba, tendremos:
Hipótesis:
Si DC // AB, entonces
Tesis: Δ ABE ~ Δ DCE
En este momento tenemos que hacer un alcance conceptual:
Cuando estudiamos la Congruencia analizamos los llamados “cuatro teoremas o criterios de congruencia de triángulos ”; pues bien, es del caso que de modo paralelo a cada uno de ellos existe un teorema o criterio de semejanza de triángulos .
Teoremas o criterios de semejanza de triángulos
Criterio de semejanza A-A-A
Si dos triángulos tienen tres ángulos cada uno respectivamente congruente con los ángulos del otro, entonces los triángulos son semejantes
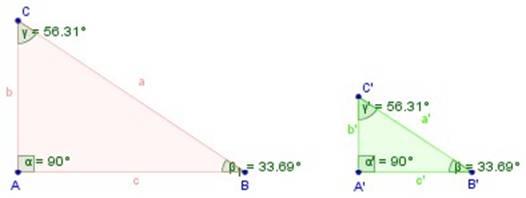
Hipótesis:
Si
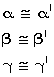 entonces
entonces
Tesis: Δ ABC ~ Δ A’B’C’
Este teorema o criterio de semejanza se puede resumir en que “Dos triángulos son semejantes cuando tienen dos ángulos respectivamente iguales (congruentes)”. El tercer ángulo resulta obligadamente igual también.
Ver: PSU: Geometría; Pregunta 11_2006
Criterio de semejanza L-L-L
Si dos triángulos tienen sus tres lados proporcionales, entonces son semejantes
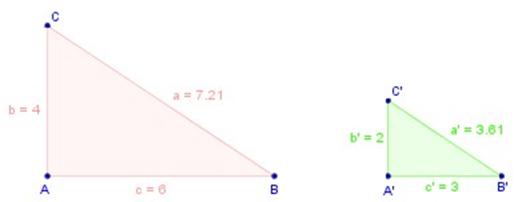
Hipótesis:
si
![]() , entonces
, entonces
Tesis: Δ ABC ~ Δ A’B’C’
Criterio de semejanza L-A-L
Si dos triángulos tienen cada uno dos lados correspondientes proporcionales y el respectivo ángulo que forman es congruente, entonces los triángulos son semejantes.
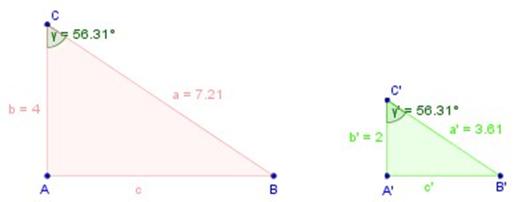
Hipótesis:
Si
![]() y, además,
y, además,
![]() , entonces
, entonces
Tesis: Δ ABC ~ Δ A’B’C’
Este criterio se puede simplificar diciendo que: Para que dos triángulos sean semejantes, basta que tengan un ángulo congruente comprendido entre lados proporcionales.
También podríamos decir que “Dos triángulos son semejantes cuando tienen un ángulo igual (congruente) y son proporcionales los dos lados que lo forman”.
Criterio de semejanza L-L-A
Para que dos triángulos sean semejantes, basta que tengan dos de sus lados respectivamente proporcionales, y que cada ángulo opuesto al mayor de esos lados sea congruente con su homólogo.
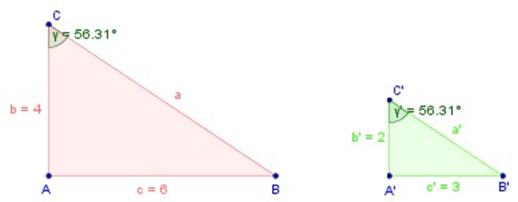
Hipótesis:
Si
![]() , y además
, y además
![]() , entonces
, entonces
Tesis: Δ ABC ~ Δ A’B’C’
Este criterio o teorema tambièn se puede expresar así: “Dos triángulos son semejantes cuando tienen dos lados respectivamente proporcionales e igual el ángulo opuesto a los lados mayores de éstos” .
Corolarios de la semejanza en triángulos
Si dos triángulos son semejantes entonces sus transversales de gravedad, sus alturas, sus perímetros, etcétera se encuentran en la misma razón que sus lados.
Si dos triángulos son semejantes entonces la razón entre sus éreas es igual al cuadrado de la razón entre sus lados.
Para tener en cuenta:
Estos cuatro teoremas de semejanza sirven a su vez para demostrar la proporcionalidad de trazos y la igualdad de ángulos.
De ellos, el primero es el que más se usa en las demostraciones; es decir, que basta encontrar dos ángulos iguales para que los triángulos que se comparan sean semejantes.
Fuente Internet:
http://rpedagogicos.galeon.com/TEOREMAS.htm
Ejercicios sobre el tema en:

