Área y perímetro del rombo

El rombo (figura que tiene los cuatro lados iguales) es un paralelógramo.

Un paralelogramo es un tipo especial de cuadrilátero (un polígono formado por cuatro lados cuyos lados son paralelos dos a dos.

Por tanto el perímetro y el área del rombo pueden calcularse como los de un paralelógramo.

Esto es:

Área del rombo

área = lado por lado (cuando conocemos el valor de su lado).

En ocasiones se conoce solo el valor de las diagonales , las que, como sabemos, son perpendiculares en un rombo. Usando esos valores también podemos calcular el área del rombo.

Si analizamos la siguiente figura

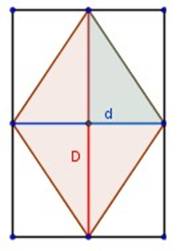
veremos que el rombo (zona coloreada) corresponde exactamente a la mitad del rectágulo que se obtiene con la proyección de sus diagonales (D y d) .

También podemos decir que los lados del rectángulo corresponden a las diagonales del rombo.

Y como el área del rectángulo se obtiene multiplicando ancho por alto (A =  D por d), entonces el área del rombo será la mitad de eso:

Dicho de otra manera: el área del rombo es igual al producto de sus diagonales dividido entre dos.

Perímetro del rombo

perímetro =  lado + lado + lado + lado

Para calcular el perímetro del rombo es necesario conocer el valor de uno de sus lados (los cuatro son iguales). Conocido ese lado ( a en la figura), el perímetro es igual a cuatro veces el valor del lado.

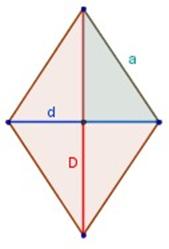
Perímetro = 4 . a

Ahora ¿cómo calculamos el valor del lado?

Para hacerlo, debemos saber que el valor de las diagonales y el del lado están relacionados.

Volvamos a la figura de arriba, en la cual aparece un triángulo coloreado en verde. Ese triángulo está formado por un cateto o lado que es la mitad de la diagonal mayor (D/2), otro cateto o lado que es la mitad de la diagonal menor (d/2) y por la hipotenusa (a), que es a su vez lado del rombo.

Entonces, recordemos, para aplicarlo, el Teorema de Pitágoras :

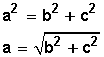
Reemplacemos los valores y tendremos

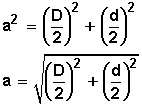
Veamos un ejemplo práctico :

Calcular el ártea y el perímetro de un rombo cuyas diagonales miden 6 m y 8 m.

Solución:

Veamos un dibujo para iniciar el análisis:

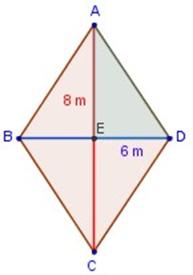
Como ya sabemos, el rombo es una figura  que tiene sus cuatro lados iguales.

El área del rombo la obtenemos usando la fórmula

, donde D es la diagonal mayor y d es la diagonal menor

reemplazamos y tenemos

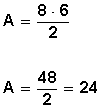
El área de dicho rombo es 24 m ²

Para calcular el perímetro, sabemos que las diagonales se cortan en el centro dividiéndose en dos trazos iguales. En este caso, dos trazos de 4 m cada uno (la diagonal de 8 m)  y dos trazos de 3 m cada uno (la diagonal de 6 m).

A su vez, esos trazos forman triángulos, de los cuales usaremos solo el que hemos coloreado con fondo verde claro (triángulo AED).

De dicho triángulo verde conocemos dos de sus lados (3 m y 4 m) y podemos calcular el valor del tercero, que en este caso corresponde a la hipotenusa de dicho triángulo).

Entonces aplicamos el Teorema de Pitágoras

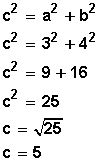
La hipotenusa de ese triágulo mide 5 m y  corresponde, además, a uno de los lados del rombo.

Conocido un lado del rombo podemos calcular su perímetro que es igual a la suma de sus cuatro lados (todos iguales):  5 + 5 + 5 + 5 = 20

El perímetro es  20 metros.

Caso del cuadrado

En el caso de un cuadrado, si solo se conoce el valor de su diagonal, se puede usar la misma fórmula del rombo (el cuadrado es un caso especial de rombo).

Ver:

Área y perímetro de un romboide

Fuente Internet:

http://www.aulafacil.com/matematicas-areas-geometria/curso/Lecc-4.htm

http://mimosa.pntic.mec.es/clobo/geoweb/area3.htm