Diagonales

Una diagonal es un segmento de recta que une un vértice interior de una figura geométrica con el vértice opuesto no consecutivo a él.  El número de diagonales que tiene un polígono cualquiera se puede calcular  mediante una fórmula matemática.

Por ejemplo :

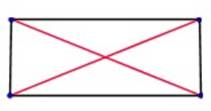
En este rectángulo se pueden trazar dos diagonales.

La fórmula para calcular el número de diagonales es:

donde n =  número de lados del polígono .

Veamos otro ejemplo:

Si tenemos un pentágono (figura de 5 lados)  ¿Cuántas diagonales se pueden trazar?

Usemos la fórmula

Y reemplacemos los valores conocidos (sabemos que aquí n = 5 )

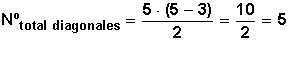
Se pueden trazar 5 diagonales.

Veamos la figura para comprobarlo:

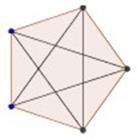
En esta figura (pentágono, un polígono de 5 lados) se pueden trazar 5 diagonales. Cuéntalas en el dibujo.

Diagonal de un rectángulo

Como ya conocemos la definición de diagonal, si la aplicamos a un rectángulo diremos que una diagonal de un rectángulo es un segmento de recta que une dos vértices no consecutivos del mismo.

Los problemas que se presentan siempre son cómo calcular el valor de diagonales en un rectángulo.

Para hacerlo, solo basta aplicar el Teorema de Pitágoras que dice que la Hipotenusa al cuadrado (la hipotenusa es la diagonal trazada) es igual a la suma de los dos catetos al cuadrado (los catetos son los otros dos lados de uno de los triangulos que se forman al trazar la diagonal, en el caso del rectángulo, uno es el ancho y otro es el largo).

>

Cálculo de la diagonal de un rectángulo

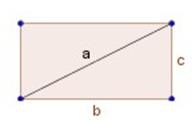
Aplicamos el Teorema de Pitágoras

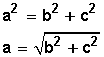
Un ejemplo práctico:

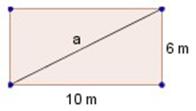
Calcular la diagonal de un rectángulo de 10 m de base y 6 m de altura.

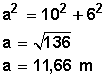
Saber calcular el valor de las diagonales en los rectángulos y cuadrados es útil para resolver problemas de cálculo de áreas y perímetros .

Fuente Internet:

http://www.geoka.net/geometria/diagonales.html