Puestas en el espacio (visualizadas en un Plano cartesiano ), dos rectas pueden ser coincidentes (una sobre la otra, formando una sola), paralelas (sin formar ángulo alguno) o pueden cortarse entre sí .

Pues bien, dos rectas que se cortan entre sí  determinan cuatro ángulos (dos pares de iguales entre sí) .

Uno de los menores de dichos ángulos se define como el ángulo entre dos rectas.

Y podemos obtener la medida de este ángulo tanto por sus pendientes como por sus vectores directores .

En este apartado veremos la representación de dos rectas y la fórmula para hallar el ángulo conociendo sus pendientes.

Antes de seguir, es conveniente repasar el tema Ecuación de la recta , para saber qué es una línea recta y su representación en un Plano Cartesiano .

Ver: Plano Cartesiano

Ver: Ecuación de la recta

Calcular ángulo entre dos rectas conocidas sus pendientes

Para calcular el ángulo entre dos rectas (l1 y l2) se debe conocer el valor de la pendiente de cada una de dichas rectas (pendientes que se identifican como m1 y m2).

Ahora es conveniente repasar el tema Recta pendiente para entender el conjunto:

Ver: Recta pendiente

Bien, volvamos a la pendiente. Cuando tenemos ese dato, o sabemos cómo obtenerlo, usaremos la fórmula

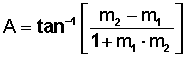
Lo cual se lee: el valor del ángulo entre dos rectas será igual a la tangente inversa (tan-1) de la fracción

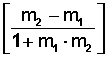
Hagamos un ejercicio de práctica:

Tenemos una recta AB (l1) cuya pendiente m1 = 1/2, que intercepta a otra recta CD (l2) cuya pendiente m2 = –1/3, encuentre el valor del ángulo que forman al cortarse.

Como es una práctica de aprendizaje, veamos la siguiente figura:

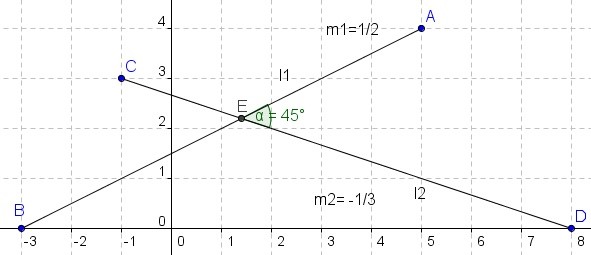
Por la magia de Geogebra vemos que el ángulo AED (α) mide 45°, pero para nuestro ejercicio ese valor no lo conocemos, veamos si lo “encontramos” usando la fórmula propuesta anteriormente:

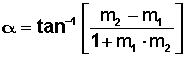
Como conocemos los valores de las pendientes, simplemente reemplazamos:

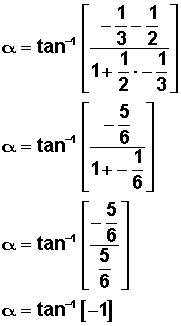
Usando la calculadora, sacamos tangente inversa de -1 y resulta 45°

Calcular ángulo entre dos rectas definidas por sus coordenadas

Como vimos cuando estudiamos la recta, hay diferentes elementos que sirven para hacer cálculos que la involucren, y uno de esos elementos es su pendiente, como explicamos en el ejercicio anterior.

Veamos ahora el siguiente caso:

Se tienen dos rectas, l1 y l2, cuyas coordenadas son los puntos A(5, 4), B(-3, 0) y C(-1, 3), D(8, 0), respectivamente. Calcular o encontrar el ángulo de la recta que forman al cortarse.

Si graficamos los datos, tenemos

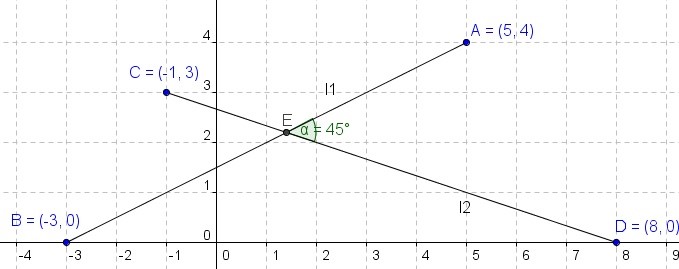
Recuerden que el ángulo de 45°, que vemos en la figura, no lo conocemos, es lo que debemos averiguar.

Aquí tenemos dos rectas (AB = l1 y CD = l2) definidas solo por pares de coordenadas .

Vaya, pero más arriba aprendimos que para calcular el ángulo entre dos rectas (l1 y l2) debemos conocer la pendiente de cada una.

Acá no está ese dato. Pero si tenemos las coordenadas de los puntos que contienen a esas rectas, podemos calcular las pendientes.

Repasar o ver: Pendiente de la recta

Si vimos la materia indicada, sobre calcular la pendiente (m), sabremos que la fórmula para hacerlo es operando con las respectivas coordenadas en la fórmula

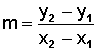
Entonces calculemos m1, para l1, cuyos puntos son

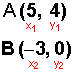
Hemos marcado en rojo cada coordenada en su respectivo eje (x e y).

Reemplazamos los valores en la fórmula

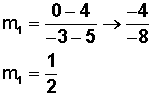
Ahora calculemos m2, para l2, cuyos puntos son

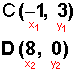
Reemplazamos los valores en la fórmula

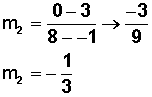
Y así tenemos que las pendientes son

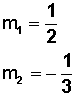
Valores que son iguales a los del ejercicio anterior en el que nos entregaban inicialmente el dato de las pendientes.

Entonces, a partir de los puntos que contienen las rectas podemos calcular las pendientes de las mismas, lo cual nos permite averiguar el valor del ángulo entre dos rectas .

Calcular ángulo entre dos ecuaciones de recta

Lo primero que debemos recordar aquí es que “la línea recta es una representación gráfica de una expresión algebraica de primer grado” ; por lo tanto, debemos calcular el ángulo entre dos expresiones algebraicas (ecuaciones).

Veamos el siguiente ejemplo:

Calcular el ángulo que forman una recta (l1) expresada como que corta a otra recta (l2) expresada como .

Como ya sabemos, para calcular el ángulo entre dos rectas debemos conocer las pendientes de ellas.

Ambas ecuaciones corresponden a la forma general o implícita de una ecuación de primer grado , que se formula como Ax + By + C = 0

Por la materia estudiada sabemos que si tenemos una recta expresada como ecuación se puede conocer su pendiente (m) usando la fórmula

Veamos qué pasa con la primera ecuación

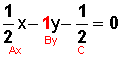
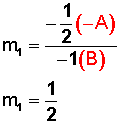
Veamos ahora qué pasa con segunda ecuación:

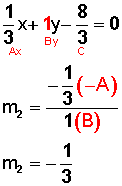
Ahora ya tenemos las dos pendientes: m1 = ½  y m2 = –1/3  y pueden calcular el ángulo entre las dos rectas (como se hizo al empezar este tema).

Ahora, Ir a:

Representación de dos rectas y la fórmula para hallar el ángulo por sus vectores.