Seguimos ahora con las ecuaciones paramétricas de la recta .

Estas se calculan a partir de la ecuación vectorial , cuya fórmula conocida es:

Obtenida ésta, procedemos a multiplicar el número t (el parámetro t, o parámetro de proporcionalidad) por las coordenadas del vector:

Ahora, sumamos ambos vectores (las coordenadas “x” entre sí, y las coordenadas “y” entre ellas), expresándolos como un solo vector:

En esta ecuación, las coordenadas de la izquierda tienen que ser iguales que las de la derecha, lo cual marcamos arriba con color, para su comprensión.

Definido esto, escribimos como una ecuación la coordenada “x” y como otra ecuación la coordenada “y”, obteniendo las ecuaciones paramétricas de una recta:

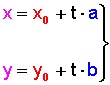
Donde Xo e Yo (en rojo) corresponden a las coordenadas del punto por donde pasa la recta:

y donde a y b (en azul) corresponden a las coordenadas de su vector de dirección:

Y donde x e y (en color magenta) son las coordenadas de la recta pedida, y cuyo valor dependerá del valor que se dé al parámetro “t”.

Ahora, con un ejercicio, veremos cómo calcular las ecuaciones paramétricas de una recta:

Ejercicio 001

Hallar las ecuaciones paramétricas de la recta que pasa por el punto Po (1, -2) y cuyo vector de dirección es v = (2, 4).

Para calcular las ecuaciones paramétricas, antes debemos calcular la ecuación vectorial:

Ahora. desarrollamos el miembro de la izquierda y multiplicamos la t por las coordenadas del vector:

Y sumamos las coordenadas de ambos vectores, expresándolas como un solo vector:

Finalmente, escribimos la ecuación de la coordenada “x” por un lado y la ecuación de la coordenada “y” por el otro, llegando a las ecuaciones paramétricas:

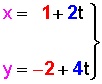
Ejercicio 002

Determinar las ecuaciones vectorial y paramétricas de la recta que pasa por el punto A (-3, -2) y tiene como vector director v (2, 3).

Primero, calculemos la ecuación vectorial, usando la fórmula de la ecuación vectorial de una recta:

Ahora, sustituimos Xo e Yo por las coordenadas del punto A, y sustituimos a y b por las coordenadas del vector director:

Y tenemos la ecuación vectorial.

A  partir de la ecuación vectorial que acabamos de obtener, multiplicamos la t por cada coordenada del vector director:

Y sumamos las coordenadas de cada vector, expresándolas en un solo vector:

Y finalmente escribimos la ecuación de la coordenada “x” y de la coordenada “y” por separado:

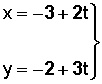
Y tenemos nuestras ecuaciones paramétricas.

Volver a:

Ecuación vectorial de la recta

Ecuaciones de la recta