Ecuación vectorial de la recta |
Ya vimos que una recta puede mostrarse visualmente (geométricamente) como una sucesión de puntos, pero también que puede definirse (algebraicamente) como una ecuación algebraica.
Esta ecuación algebraica de la recta puede expresarse de varias maneras, según los datos iniciales que conozcamos de ella.
Una de estas formas es mediante una ecuación vectorial .
Las otras formas de expresar la ecuación de una recta , podemos repasarlas en:
Ver: http://www.profesorenlinea.cl/geometria/Recta_Ecuacion_de.html
Pero, sigamos con la Ecuación vectorial de la recta :
Para encontrar la ecuación vectorial que defina una recta se necesita conocer un punto (Po) de la misma, dado por sus coordenadas (Xo e Yo), y un vector director (v) de dicha recta, también dado por sus coordenadas (a, b).
Recordemos que un vector director es un vector que indica la dirección y el sentido de una recta, y que sus coordenadas de inicio siempre serán (0, 0) y las de término, las indicadas en cada caso (a, b).
Aunque visualmente, en cada ejercicio, las coloquemos encima de la recta por conocer (recuerden que un vector se puede trasladar a cualquier parte del plano).
Entonces, veamos cómo debemos operar para obtener la ecuación vectorial de una recta que pasa por el punto conocido Po, cuyas coordenadas son Xo e Yo:
Lo anotamos así:
![]()
y señalamos que su vector de dirección es
![]()
Como vemos en el gráfico de abajo
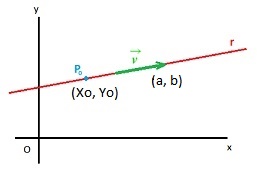
Nota: algunas fuentes educativas identifican el vector (v) como (u). Además, debemos recordar que algebraicamente un vector se identifica solo con las coordenadas de su término (donde se marca la flechita), por eso nuestro vector es
![]()
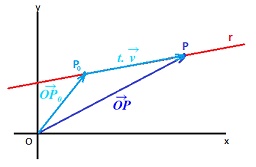
Para completar nuestra explicación gráfica, en la recta r , marcamos o elegimos un punto cualquiera de ella; por ejemplo, el punto P, que se identificará por sus coordenadas x e y (que corresponden a nuestra incógnita y que indicará hasta qué coordenadas llega la recta):
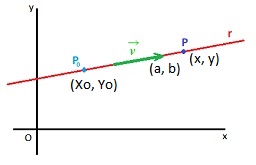
Entonces, geométricamente, una ecuación vectorial quedará determinada por el
vector OP
; que nace en el origen de coordenadas (O) y llega al punto P, perteneciente a la recta:
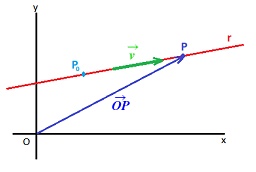
Recordemos que la
suma y la resta de vectores
se pueden realizar en forma geométrica, pero también se pueden calcular de manera algebraica o matemática como veremos más abajo.
Si hacemos la suma geométrica de vectores , veremos que este vector OP corresponde a la suma vectorial del vector OPo más el vector PoP, siendo el vector OPo un vector que nace en el origen de coordenadas y llega al punto Po, y el vector PoP un vector con origen en el punto Po y extremo en el punto P:
![]()
Ver: Vectores en el Plano Cartesiano
Suma geométrica que gráficamente veríamos como:
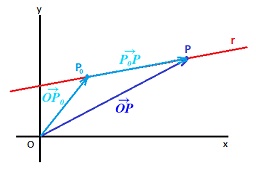
Por otro lado, el vector PoP, lo podemos expresar en función del vector de dirección de la recta (v), multiplicado por un número (t), tal que lo convierta en un vector con la longitud requerida:
![]()
Nota: Fuentes educativas distintas utilizan lambda (λ) o la letra (k) para identificar este parámetro que nosotros llamamos (t). Recordemos, además, que (t) puede ser cualquier número real y dependiendo de su valor conoceremos las coordenadas del punto (P), con la cual queda definida la recta que buscamos.
Hecha la suma geométrica de vectores, la ecuación vectorial queda expresada con la siguiente fórmula:
![]()
Fórmula que podemos expresar algebraicamente, en función de las coordenadas que definen a cada vector, de la siguiente manera:
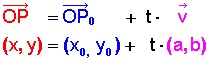
Como vemos, cada vector se ha identificado ahora por su par de coordenadas (según los colores, para su mejor comprensión) y obtenemos la fórmula algebraica que utilizaremos para calcular la ecuación vectorial de cualquier recta, conociendo su vector de dirección (a, b) y un punto por donde pase (Xo, Yo), a lo que agregamos el valor del parámetro (t), que es un número perteneciente al conjunto de los números reales, para llegar a definir el punto término (x, y) de nuestra recta.
Aunque la demostración resulte algo confusa, veremos que hallar la ecuación vectorial es muy sencillo.
Veámoslo en el siguiente ejemplo:
Hallar la ecuación vectorial de la recta que pasa por el punto Po (3, -4) y cuyo vector de dirección es v = (2, 3).
Según los datos del enunciado, la recta pasa por el punto: Po (3, -4)
Y tiene como vector de dirección: v = (2, 3)
Para obtener la ecuación vectorial de esta recta, en la fórmula
![]()
Colocamos los valores de las coordenadas que conocemos:
![]()
Y ya tenemos la ecuación vectorial de la recta buscada.

