Para trabajar el tema, es imprescindible conocer las características de los polígonos.

Previamente, ver:

https://www.profesorenlinea.cl/geometria/Poligono1.htm

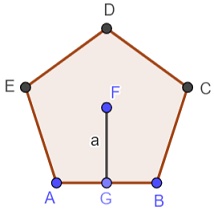
Un polígono regular, como el pentágono de arriba, o cualquier polígono regular, está inscrito en una circunferencia cuando todos sus vértices (ABCDE) son puntos de la circunferencia y todos sus lados están incluidos dentro del círculo que ésta define.

Sabido esto, podemos empezar a operar para calcular el perímetro y luego el área de un polígono regular.

Perímetro (p) de un polígono regular

Se calcula fácilmente solo multiplicando el valor de un lado por la cantidad de lados que tenga el polígono.

p = l * n

donde n es la cantidad de lados del polígono.

Área (A) de un polígono regular

Siendo un poquito más complicado, igual es muy fácil lograrlo.

Si nos dan el valor de un lado (l)  y el valor de la apotema (a), resulta muy sencillo calcular el área usando la fórmula

El área del polígono es igual al perímetro por la apotema dividido entre 2

Recordando que la apotema (a) es la  Perpendicular entre el centro de un polígono regular y uno cualquiera de sus lados, al que divide en dos partes iguales, como se ve en la figura superior.

Veamos un ejemplo:

Calcular el perímetro y el área del octágono de la figura, cuyo lado mide 9,7 cm y su apotema mide 8 cm.

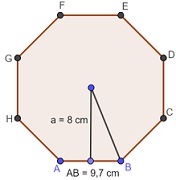
Solución:

Datos que tenemos

Lado (l)  = 9,7 cm

Entonces ½ lado =  4,85 cm

Cantidad de lados = 8

Apotema (a) = 8 cm

Perímetro (p) = 9,7 * 8 = 77,6 cm

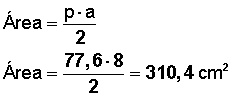
Calcular la apotema

El problema se enreda un poco cuando solo nos dan el valor de un lado y, para obtener el área, tenemos que calcular la apotema.

Veamos un ejemplo:

Dado el polígono (pentágono)

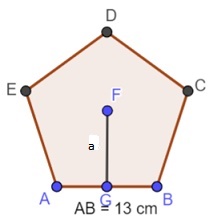
Del cual nos entregan solo el valor de su lado = 13 cm

Primero, necesitamos conocer el valor del ángulo α (figura siguiente) para saber el valor de su tangente.

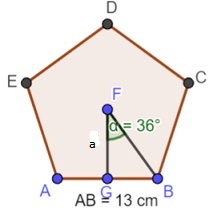
En la figura anotamos que α mide 36°, y para llegar a ese valor usamos la fórmula

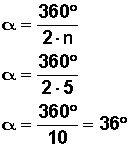
360° es el valor del ángulo del entro en la circunferencia.

Donde n es el número de lados del polígono; en este caso, un pentágono tiene 5 lados

Conocido el valor del ángulo α  (36°), debemos recurrir a las razones trigonométricas.

Como tenemos el valor del cateto opuesto (6,5 cm, la mitad del lado conocido, ya que la apotema lo divide en dos partes iguales), usaremos la razón de la tangente:

La tangente de un ángulo α de un triángulo rectángulo se define como la razón entre el cateto opuesto al ángulo α y el cateto contiguo al mismo ángulo o cateto adyacente.

Tangente es una de las razones trigonométricas. Se llaman razones porque se expresan como el cociente de dos de los lados del triángulo rectángulo.

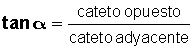
tang 36° = 0,73 (valor que obtenemos con una calculadora).

El cateto adyacente o contiguo es la apotema.

Y  la fórmula para calcular la apotema es

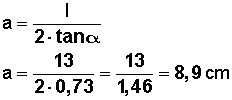
apotema (a) = lado del polígono dividido entre 2 por tangente de α.

Entonces:

Perímetro = 13 * 5 = 65 cm

El área (A) será

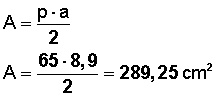
 (perímetro por apotema dividido entre 2)

Camino alternativo

Otro camino para calcular o conocer la apotema de un polígono regular sería trabajar con el valor de un ángulo interior.

Ángulos interiores de un polígono regular

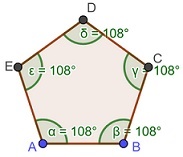
Si n es el número de lados de un polígono:

Suma de Ángulos Interiores = (n − 2) × 180°

Entonces, cada ángulo interior (de un polígono regular) será

Con esta fórmula podemos calcular el valor de un ángulo interior de cualquier polígono regular.

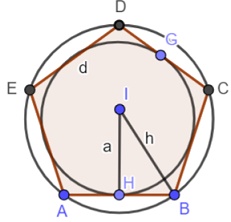
Conocer ese ángulo interior nos permitirá calcular luego tanto el radio de la circunferencia circunscrita donde se inscribe el polígono (que será la hipotenusa de éste), como el radio de la circunferencia inscrita (que será la apotema del polígono).

En la figura superior trazo (IH) es la apotema y coincide con ser el radio de la circunferencia inscrita en el polígono. A su vez, el trazo (IB) es la hipotenusa del triángulo rectángulo que se forma y coincide con ser el radio de la circunferencia circunscrita al polígono.

También vemos que el trazo (HB) corresponde a la mitad de lado conocido, siendo además el cateto adyacente al ángulo α (ángulo que puede llamarse con cualquier símbolo griego).

Con estos datos, podemos calcular el valor del radio de la circunferencia circunscrita (insistimos, que es la hipotenusa) usando relaciones o razones trigonométricas:

Por trigonometría sabemos que

cos α = lado adyacente/ hipotenusa

hipotenusa = lado adyacente / cos α

Para el radio de la circunferencia inscrita (la apotema) usaremos

tan α = lado opuesto (FG) / lado adyacente (GB)

lado opuesto (FG) = lado adyacente (GB) * tan α

Y ese será el radio o apotema pedido.

Veamos el siguiente ejemplo:

Calcular la apotema y la hipotenusa de un pentágono de 6 cm de lado.

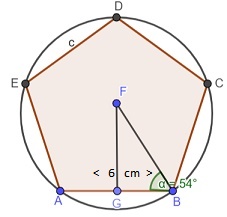
Solución

Aunque aparece en la figura, previamente no conocemos el valor del ángulo α, que es la mitad de un ángulo interior de un polígono (pentágono en nuestro ejemplo).

Lo averiguamos con la fórmula que ya vimos

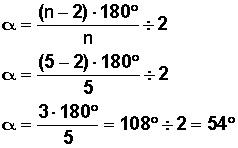
108° mide cada ángulo interior de un pentágono; entonces α, que es la mitad, vale 54°.

Recurramos a las razones trigonométricas:

Para calcular la hipotenusa usaremos

cos α = lado adyacente (GB)/ hipotenusa (FB)

cos 54° = lado adyacente (GB) / hipotenusa (FB)

si cos 54° = 0,59

entonces

0,59 = 3 / hipotenusa (FB)

hipotenusa (FB) = lado adyacente (GB) / cos α

hipotenusa (FB) = 3/0,59 = 5,08 cm

Como vemos, ya tenemos un lado del triángulo (3 cm) y la hipotenusa (5,08 cm) con lo cual, usando el Teorema de Pitágoras (c² = a² + b²) podríamos calcular la apotema.

Pero, para calcular la apotema usaremos de nuevo la trigonometría:

Recordemos que α vale 54°.

tan α = lado opuesto (FG)/ lado adyacente (GB)

tan 54° = lado opuesto (apotema) / lado adyacente (medio lado)

tan 54° = 1,38 (obtenido con una calculadora).

1,38 = lado opuesto (apotema) / 3

1,38 = a/3

a = 3 * 1,38 = 4,14 cm

Si dejamos la hipotenusa en 5 cm, la apotema en 4 cm y tenemos el lado de 3 cm;

Podemos comprobar con el Teorema de Pitágoras, que

c² = a² + b²

5² = 4² + 3²

25 = 16 + 9

Apotema de un hexágono

Calcular la apotema y la hipotenusa de un hexágono de 6 cm de lado.

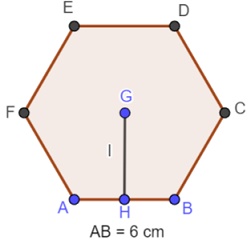
Solución:

Trabajaremos con el ángulo α a partir del ángulo del centro.

Primero, necesitamos conocer el valor del ángulo α

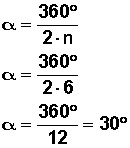
También sabemos que la mitad del lado es 3 cm (la apotema lo divide en dos).

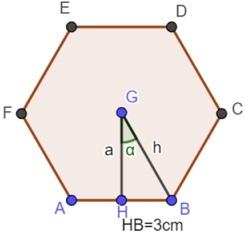
Entonces, usamos la razón tangente de α:

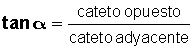
tan 30° = 0,58 (valor que obtenemos con una calculadora).

Cateto opuesto = 3 cm

El cateto adyacente o contiguo es la apotema.

Entonces

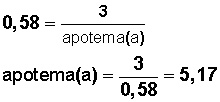
Otra fórmula para calcular la apotema es

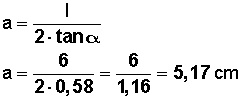
apotema (a) = lado del polígono dividido entre 2 por tangente de α.

Respuesta: apotema = 5,17 cm

Complementariamente, c,lculemos el perímetro y el área del hexágono regular dado:

El perímetro (p) será

Respuesta: p = 6 * 6 = 36 cm

Entonces:

El área (A) será

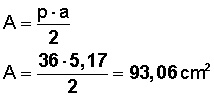
 (perímetro por apotema dividido entre 2)

Ahora, calculemos la hipotenusa del mismo triángulo:

Para ello, usaremos:

Ángulo interior, el cual calculamos

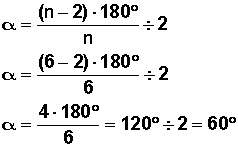
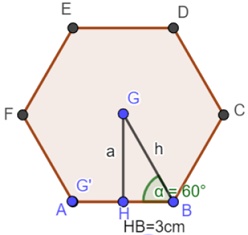
Recurramos a las razones trigonométricas:

Para calcular la hipotenusa usaremos

cos α = lado adyacente (HB)/ hipotenusa (GB)

cos 60° = lado adyacente (HB) / hipotenusa (GB)

si cos 60° = 0,5

entonces

0,5 = 3 / hipotenusa (GB)

hipotenusa (GB) = lado adyacente (HB) / cos α

hipotenusa (GB) = 3/0,5 = 6 cm

Y así vemos que en el hexágono regular la hipotenusa tiene el mismo valor que un lado del polígono.