Obtener la Ecuación de la circunferencia con centro (C) fuera del origen de las coordenadas |
Tomemos, por ejemplo, la circunferencia cuyo centro está dado por C (2, ─3), con radio r = 5 que se muestra en la figura
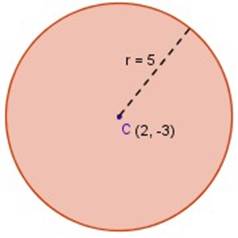
Para obtener la ecuación general de la circunferencia que estamos viendo podemos usar dos métodos:
Método por desarrollo y
Método con las fórmulas conocidas.
Método por desarrollo
Como conocemos el centro, C (2, ─3) y el radio (r = 5) entonces la fórmula ordinaria de la circunferencia será
(x ─ a) 2 + (y ─ b) 2 = r 2 donde a y b son las coordenadas del centro C (a, b), que en nuestro caso corresponde a C (2, ─3)
entonces, nuestra ecuación ordinaria quedará como
(x ─ 2) 2 + (y ─ ─ 3) 2 = 5 2
(x ─ 2) 2 + (y + 3) 2 = 5 2
(x ─ 2) 2 + (y + 3) 2 = 25
Nota:
algunos usan otras letras, como
(x ─ h)
2
+ (y ─ k)
2
Sigamos.
Tenemos nuestra ecuación ordinaria
(x ─ 2) 2 + (y + 3) 2 = 25
y desarrollamos sus dos binomios:
(x ─ 2) (x ─ 2) + (y + 3) (y + 3) = 25
(x 2 ─ 2x ─ 2x + 4) + (y 2 + 3y + 3y + 9) = 25
(x 2 ─ 4x + 4) + (y 2 + 6y + 9) = 25
Recordemos que la estructura de la ecuación general de la circunferencia es
x 2 + y 2 + Dx + Ey + F = 0
Entonces, ordenamos nuestra ecuación anterior y la acomodamos de acuerdo con la fórmula general:
x 2 + y 2 ─ 4x + 6y + 4 + 9 ─ 25 = 0
x 2 + y 2 ─ 4x + 6y ─ 12 = 0
que es la ecuación general de la circunferencia con centro en las coordenadas 2, ─3 y cuyo radio es 5.
Método con las fórmulas conocidas
Como conocemos el centro, C (2, ─3) y el radio (r = 5) entonces aplicamos las fórmulas
Si
![]() entonces D = ─ 2a
entonces D = ─ 2a
Si
![]() entonces E = ─ 2b
entonces E = ─ 2b
Si
![]() entonces F = a
2
+ b
2
─ r
2
entonces F = a
2
+ b
2
─ r
2
Recordemos que C (2, ─3) corresponde a C (a, b)
Entonces, hacemos:
![]()
![]()
![]()
F = 4 + 9 ─ 25 = ─12
Si recordamos que la estructura de la ecuación general de la circunferencia es
x 2 + y 2 + Dx + Ey + F = 0
y en ella sustituimos los valores ahora conocidos de D, E y F, tendremos
x 2 + y 2 + ─4x + 6y + ─12 = 0
x 2 + y 2 + ─4x + 6y ─12 = 0
obtenemos la misma ecuación general de la circunferencia que logramos mediante el método del desarrollo.
Ahora, hagamos algunos ejercicios
Ejercicio 1
Encuentre la ecuación general de la circunferencia cuyo centro está en las coordenadas
![]() y que tiene un radio igual a
y que tiene un radio igual a
![]() .
.
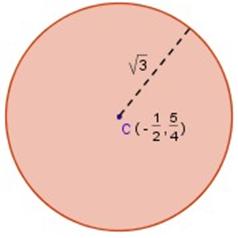
Resolución por desarrollo
En este caso podemos usar las fracciones o convertirlas a decimales:.
Como el centro no está en el origen vamos a usar la fórmula ordinaria para llegar a la desarrollada:
Para hacerlo, partamos de aquí:
![]()
(x ─ a) 2 + (y ─ b) 2 = r 2
|
Nota: Debemos recordar que x e y corresponden a las coordenadas de cualquier punto en la circunferencia, P (x, y) , distante un radio desde el centro. |
Volvamos a la fórmula:
Reemplacemos los valores en las coordenadas del centro, C (a, b):
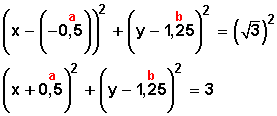
y aquí tenemos la ecuación ordinaria (formada por dos cuadrados de binomio) la cual ahora desarrollaremos para llegar a la ecuación general:
|
Recordemos el cuadrado del binomio: a 2 + 2ab + b 2 Primer término al cuadrado (x) 2 , más el doble del producto del primero por el segundo término 2(x)(0,5), más el cuadrado del segundo término (0,5) 2 |
Pongamos los valores de nuestros binomios al cuadrado:
(x) 2 + 2(x)(0,5) + (0,5) 2 + (y) 2 + 2(y)(─1,25) + (─1,25) 2 = 3
x 2 + x + 0,25 + y 2 ─2,50y + 1,56 = 3
ahora acomodamos los términos e igualamos a cero, para obtener la ecuación general :
x 2 + y 2 + x ─ 2,50y + 0,25 + 1,56 ─ 3 = 0
x 2 + y 2 + x ─ 2,50y ─ 1,19 = 0
Resolución por el sistema de fórmulas conocidas
Tenemos:
Centro de la circunferencia (coordenadas)
![]()
Radio
r =
![]()
Y las fórmulas
D = ─2a
E = ─2b
F = a 2 + b 2 ─ r 2
Recuerde que la ecuación general de la circunferencia tiene esta estructura:
x 2 + y 2 + Dx + Ey + F = 0
Por lo que solo debemos calcular D, E y F
![]()
![]()
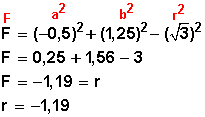
![]()
![]()
![]()
Ahora que ya conocemos D, E y F los acomodamos en la fórmula general y tendremos:
x 2 + y 2 + x + ─2,50y + ─1,19 = 0
x 2 + y 2 + x ─ 2,50y ─ 1,19 = 0 fórmula general de la circunferencia dibujada arriba.
|
Importante Los dos métodos utilizados aquí para encontrar la ecuación de la circunferencia nos indican que si nos dan las coordenadas del centro de una circunferencia distintas de cero y el radio de la misma conviene usar el método de las fórmulas. No obstante, si alguien quiere saber exactamente cómo se procede, puede usar el sistema del desarrollo. |
Ejercicio 2
Hallar la ecuación general de la circunferencia con centro en C (1, 3) y radio r = 4 .
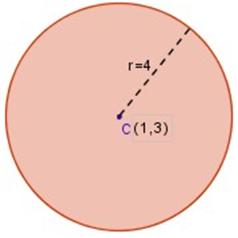
Resolución
Sabemos que debemos obtener un ecuación de la forma
x
2
+ y
2
+ Dx + Ey + F = 0
por lo que necesitamos saber cuánto valen
D, E
y
F
Para ello, recordamos que
D = ─2a
E = ─2b
F = a 2 + b 2 ─ r 2
Sustituyendo en D y E los valores que nos entregan las coordenadas del centro C (1, 3) , donde
a = 1
b = 3
tendremos que
D = ─2(1) = ─2
E = ─2(3) = ─6
Y ahora sustituimos en
F = a 2 + b 2 ─ r 2
F = (1) 2 + (3) 2 ─ (4) 2
F = 1 + 9 ─ 16
F = ─6
Como ya tenemos los valores de
D = ─2
E = ─6
F = ─6
Los usamos para sustituir en la ecuación
x 2 + y 2 + Dx + Ey + F = 0
para quedar
![]()
y llegar finalmente a
x 2 + y 2 ─ 2x ─ 6y ─ 6 = 0 como la fórmula general de la circunferencia dibujada arriba.
Ejercicio 3
Hallar la ecuación general de la circunferencia que pasa por el punto P (─3, 2) y cuyo centro es el punto C (1, 5)
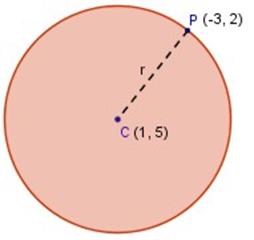
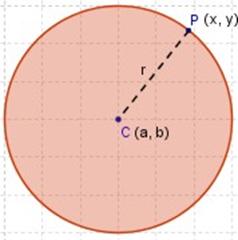
Resolución
Debemos calcular el radio (ya que no lo conocemos), pero como tenemos las coordenadas de un punto y del centro podemos calcularlo así:
El radio es la distancia de C a P , y como su fórmula para conocer dicha distancia es
![]()
Hacemos
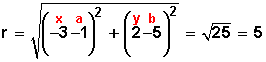
Ahora tenemos ubicado el centro C (1, 5) y el radio r = 5
y acudimos a la fórmula ordinaria de la circunferencia
(x ─ a) 2 + (y ─ b) 2 = r 2
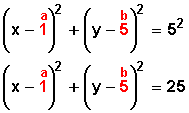
Desarrollamos los cuadrados de los binomios
(x 2 + ─x + ─x + 1) + (y 2 + ─5y + ─5y + 25 = 25
x 2 ─ 2x + 1 + y 2 ─ 10y + 25 = 25
x 2 + y 2 ─ 2x ─ 10y + 1 + 25 ─ 25 = 0
x 2 + y 2 ─ 2x ─ 10y + 1 = 0
|
Nota importante: En este ejercicio conocemos las coordenadas de uno de los puntos de la circunferencia, P (─3, 2) pero ese dato nos sirvió solo para calcular el radio. Conocido éste, la fórmula general que obtendremos ahora servirá para todos los puntos de la circunferencia equidistantes del centro, representados como P (x, y), por eso en la fórmula ordinaria de la circunferencia reemplazaremos solo los valores de a y de b como las coordenadas del centro C (1, 5) |
Ejercicio 4
Hallar la ecuación general de la circunferencia cuyo diámetro es el segmento entre los puntos A(2, 3) y B(─4, ─9)
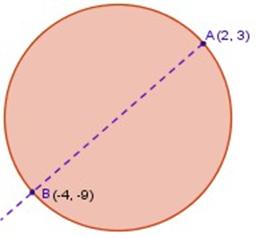
Resolución
Como el segmento AB es el diámetro , el centro estará en la mitad de este (radio), y hacemos
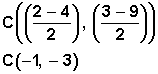
Ahora calculamos el radio, que es la distancia desde C(─1, ─3) hasta el punto A(2, 3)
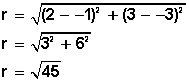
Conocemos ahora las coordenadas del centro C(─1, ─3) y el radio
![]()
Aplicamos la fórmula ordinaria
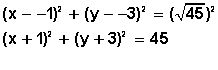
Desarrollamos los binomios
(x 2 + x + x + 1)+ (y 2 +3y + 3y + 9) = 45
(x 2 +2x +1) + (y 2 + 6y + 9) = 45
x 2 + y 2 +2x +6y +1+ 9 ─45 = 0
x 2 + y 2 +2x +6y ─ 35 = 0 ecuación de la circunferencia graficada arriba.
Como un ejercicio probatorio de la efectividad de la fórmula analítica x 2 + y 2 +2x +6y ─ 35 = 0 reemplacemos los valores de las coordenadas de los puntos A y B en x e y
Primero el A(2, 3) que sea x = 2, y = 3
2 2 + 3 2 + 2•2 + 6•3 ─ 35 = 0
4 + 9 + 4 + 18 ─ 35 = 0
Ahora el B(─4, ─9) que sea x = ─4, y = ─9
(─4) 2 + (─9) 2 + 2(─4) + 6(─9) ─ 35 = 0
16 + 81 ─ 8 ─ 54 ─ 35 = 0
Ejercicio 5
Hallar la ecuación de la circunferencia centrada en el punto (5, ─2) y de radio 3.
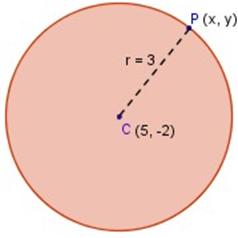
Resolución
Recordemos nuestra ecuación ordinaria de la circunferencia:
(x ─ a) 2 + (y ─ b) 2 = r 2
Conocemos a y b (5, ─2) y el radio (r = 3)
Entonces reemplacemos
(x ─ 5) 2 + (y ─ ─2) 2 = 3 2
(x ─ 5) 2 + (y + 2) 2 = 9
Desarrollemos lo binomios cuadrados:
(x ─ 5) (x ─ 5) + (y + 2) (y + 2) = 9
(x 2 ─ 10x + 25) + (y 2 + 4y + 4) = 9
ordenamos e igualamos a cero
x 2 + y 2 ─ 10x + 4y + 25 + 4 ─ 9 = 0
x 2 + y 2 ─ 10x + 4y + 20 = 0
Ejercicio 6
Calcular la ecuación de la circunferencia de centro (1, 1) y que contiene al punto (–2, 3).
Resolución:
Primero debemos conocer el radio
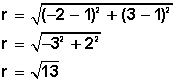
Entonces la ecuación ordinaria nos queda
![]()
x 2 ─ 2x + 1 + y 2 ─ 2y + 1 = 13
x 2 + y 2 ─ 2x ─ 2y + 1 + 1 ─ 13 = 0
x 2 + y 2 ─ 2x ─ 2y ─ 11 = 0
Ir a:
Dada la ecuación general de la circunferencia, obtener su centro y el radio

