Dada la ecuación general de una circunferencia, obtener su centro y el radio

Para entrar en materia, tenemos la siguiente ecuación general de una circunferencia :

x ² + y ² − 3x + 4y − 1 = 0

a partir de ella podemos encontrar  el centro y el radio de esa circunferencia.

Para hacerlo, existen dos métodos:

Primer método

La ecuación general dada la vamos a convertir en dos binomios al cuadrado igual a r ² , que es la forma de la ecuación ordinaria ,

De nuevo conviene recordar que un binomio al cuadrado se escribe como

(a + b) 2 , que dasarrollado queda como (a + b) + (a + b) a 2 + ab +ab + b 2 a 2 + 2ab + b 2 Primer término al cuadrado (x) 2 , más el doble del producto del primero por el segundo término  2(x)(0,5), más el cuadrado del segundo término (0,5) 2

Aquí debemos fijar nuestra atención en el término 2ab, que está precedido por el 2 y tiene ab (sin elevar al cuadrado), siendo a el primer término y b el segundo del binomio. Este término ( b ) será clave para poder completar los 3 términos que genera el binomio al cuadrado (a + b) ² = a ² + 2ab + b ²

Volviendo a nuestra ecuación general, debemos saber que en ella la x corresponde al primer término  −la a de (a + b) ² − y la y corresponde al segundo −la b de (a + b) ² −

Reiteramos nuestra ecuación general:

x ² + y ² − 3x + 4y − 1 = 0 y vamos a separar sus términos para darle forma de dos binomios al cuadrado desarrollados:

Deberíamos obtener algo como:

, entendido como la suma de dos binomios al cuadrado, donde en cada binomio encontramos:

el cuadrado del primer término (del binomio) ( x ² en uno e y ² en el otro)

el doble producto del primer término por el segundo  ( −3x en uno y +4y en el otro)

el cuadrado del segundo término (del binomio) (+/− ¿?) en ambos cuadrados y que es ese tercer término que debemos deducir para cada cuadrado del binomio.

Este tercer término, lo obtendremos del −3x para un binomio y del +4y para el otro.

Respecto a −3x, sabemos que corresponde al segundo término del binomio desarrollado , generalizado como 2ab.

Ahora, si tenemos vemos que la x (a) está al cuadrado en x ² (a ² ) y lineal en x (a) , entonces el −3 corresponde a 2b (el segundo término lineal en 2ab ).

Y hacemos

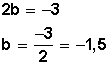
Ya conocemos b , entonces lo ponemos en nuestra fórmula

Hacemos lo mismo para el segundo binomio:

Si tenemos vemos que la y (a) está al cuadrado en y ² (a ² ) y lineal en y (a) , entonces el +4 corresponde a 2b (el segundo término lineal en 2ab ).

Y hacemos

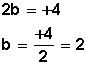
Ahora completamos la fórmula

(x ² − 3x + 2,25) + (y ² + 4y + 4) = 1

Ahora, como en el lado izquierdo de la ecuación agregamos +2,25 y +4 , para mantenerla equilibrada debemos agregar lo mismo en el lado derecho:

(x ² − 3x + 2,25) + (y ² + 4y + 4) = 1 + 2,25 + 4

(x ² − 3x + 2,25) + (y ² + 4y + 4) =  7,25

Y ahora tenemos dos trinomios , los cuales nos generarán dos binomios al cuadrado, de la forma:

(x − 1,5) ² + (y + 2) ² = 7,25

Que es la ecuación ordinaria de la circunferencia , y de donde obtendremos las coordenadas del centro y el valor del radio.

Recordemos la estructura de la ecuación ordinaria:

(x − h) ² + (y − k) ² = r ²

Reemplazamos y queda

(x − − 1,5) ² + (y − + 2) ² = r ²

(x  + 1,5) ² + (y − 2) ² = 7,25

Ecuación que nos dice lo siguiente:

La x y la y representan a las coordenadas de cualquier punto sobre la circunferencia equidistante del centro.

Los valores 1,5 y −2 representan las coordenadas del centro de la circunferencia anterior

El valor 7,25 representa a r ² , por lo tanto

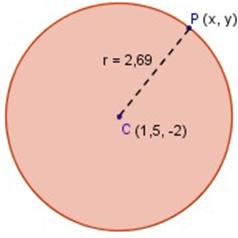
Entonces, la ecuación general x ² + y ² − 3x + 4y − 1 = 0

corresponde a una circunferencia con centro  C(1,5 ,  −2) cuyo radio es ≈ 2,69 como la que vemos en la figura.

Ecuación general de la circunferencia de arriba: x 2 + y 2 − 3x + 4y − 1 = 0

Segundo método

Lo llamaremos método de fórmulas conocidas .

Reiteramos nuestra ecuación general:

x ² + y ² − 3x + 4y − 1 = 0 y para este método utilizaremos solo fórmulas (que debemos recordar o conocer):

Primero, recordemos la estructura de la ecuación ordinaria :

(x − h) ² + (y − k) ² = r ²

Recordemos que en esta ecuación la x y la y representan las coordenadas de cualquier punto de la circunferencia que equidiste un radio desde el centro, y que h y k representan las coordenadas del punto central de la circunferencia (también se utiliza a y b para identificarlas)

Es a partir de esta ecuación que se obtienen las fórmulas que usaremos:

También tenemos que recordar que la estructura de la ecuación general de la circunferencia la podemos expresar como

x ² + y ² + Dx + Ey + F = 0

Y si la comparamos con la ecuación dada tendremos

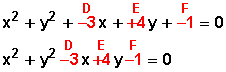
donde vemos que

D vale −3

E vale +4

F vale −1

y con estos datos y con las fórmulas de arriba vamos a conocer las coordenadas del centro:

Nuestra circunferencia tiene centro en las coordenadas (1,5,  −2)

Con los mismos datos calculamos ahora el radio de la circunferencia:

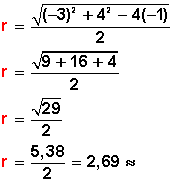
Nuestra circunferencia tiene un radio ≈ 2,69 y sus coordenadas del centro C(1,5,  −2)

Ejercicio 1

Calcular el centro y el radio de la circunferencia x ² + y ² + 2x − 4y − 4 = 0

Recordemos la estructura de la ecuación general:

x ² + y ² − 2ax − 2by + a ² + b ² − r ² = 0

Que sintetizada queda

x ² + y ² +  Dx  + Ey + F = 0

Desarrollemos la ecuación

x ² + y ² + 2x − 4y − 4 = 0

x ² + y ² + 2x − 4y = 4

Busquemos los dos binomios al cuadrado

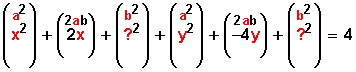
El tercer término que falta en el primer binomio se obtiene de

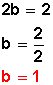
Y el tercer término que falta en el segundo binomio se obtiene de

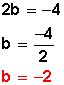
Asi formamos:

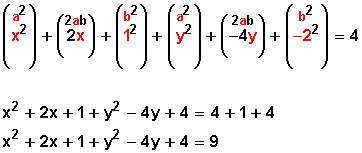
Vemos que al lado izquierdo agregamos +1 y +4 (los terceros términos de los binomios) por ello agregamos los mismos valores a la derecha de la ecuación, para equilibrarla.

Ahora  partir de estos dos trinomios podemos definir dos binomios al cuadrado:

(x + 1) ² + (y − 2) ² = 9

que, como vemos, se asemeja a nuestra ecuación ordinaria de la forma

(x − h) ² + (y − k) ² = r ²

Si comparamos, resulta que

h = +1

k = −2

Reemplazamos y tenemos

(x − +1) ² + (y − −2) ² = r ²

(x − 1) ² + (y + 2) ² = 9

(x − 1) ² + (y + 2) ² = 3

Respuesta:

Las coordenadas del centro de la circunferencia dada son (─1, 2) y su radio es igual a 3 .

Usemos el método de las fórmulas .

Conocemos la estructura de la ecuación ordinaria :

(x − h ) ² + (y − k ) ² = r ²

Conocemos las fórmulas

Estructura de la ecuación general de la circunferencia:

x ² + y ² + Dx + Ey + F = 0

La comparamos con la ecuación dada, y tendremos

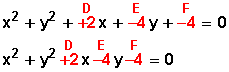
donde vemos que

D vale +2

E vale −4

F vale −4

Reemplacemos en las fórmulas:

Nuestra circunferencia tiene centro en las coordenadas (−1,  2)

Y su radio es

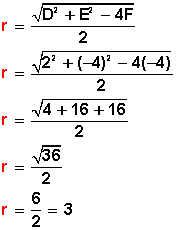
Nuestra circunferencia tiene un radio igual a 3

Ir a:

Ecuación de la circunferencia