Cálculo de perímetro y área en figuras sombreadas

Una figura sombreada es una figura geométrica no convencional, y se produce por la superposición de dos o más figuras geométricas tradicionales.

Para calcular las áreas sombreadas hay que calcular el área de cada una de las figuras y restar una de la otra.

Para comprender bien, lo mejor es partir con ejemplos simples:

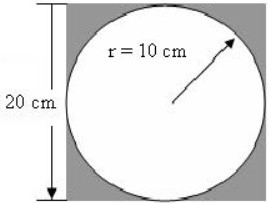
En la figura, tenemos que calcular el área de la parte sombreada. Vemos que esta se obtiene de la superposición de un círculo dentro de un cuadrado.

Entonces, tenemos que calcular el área del cuadrado y a esta restarle el área del círculo.

Repasar: Área de figuras geométricas

Calculemos:

Área del cuadrado: A = L x L   → 20 x 20 = 400 cm ²

Área del círculo:      A  = ∏r ² → 3,1416 (10) ² → 3,1416 (100) →314,16 cm ²

Entonces, al área del cuadrado le restamos el área del círculo y tenemos

400  ̶  314,16  = 85,84 cm ² es el área sombreada.

Veamos otro ejemplo:

Calcular el área sombreada de la figura:

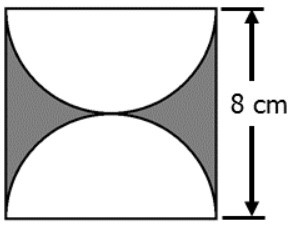
Vemos que sobre un cuadrado de 8 cm de lado se han superpuesto dos semicírculos cuyo diámetro es 8 cm.

Calculemos:

Área del cuadrado:  A = L x L → 8 x 8 = 64 cm ²

En realidad, los dos semicírculos forman un círculo completo, por ello calculamos:

Como el diámetro del círculo es 8 cm, su radio será 4 cm.

Área del círculo:       A  =  ∏r ² → 3,1416 (4) ² → 3,1416 (16) → 50,27 cm ²

Ahora, al área del cuadrado le restamos el área del círculo y tenemos

64  ̶  50,27 = 13,73 cm ² es el área sombreada.

Ir a: Áreas sombreadas: Ejercicios

Ver:

https://www.youtube.com/watch?v=wPyM5UZDa5c

https://es.slideshare.net/diomeposada/calculo-de-areas-sombreadas

http://matematica1.com/perimetros-y-areas-de-regiones-sombreadas-ejercicios-de-geometria-de-sexto-de-primaria/