La ecuación de continuidad

Esta ecuación expresa la idea de que la masa de fluido que entra por el extremo de un tubo (ducto) es la misma que debe salir por el otro extremo. Si dicha masa (volumen) pasa por secciones de diámetros diferentes (áreas diferentes), variará su velocidad, pero la masa será la misma, por unidad de tiempo, a la salida del ducto.

Veamos:

Si un fluido fluye (se desplaza) desde la sección 1 hacia la sección 2 (con diámetro distinto) con rapidez constante; es decir, si la cantidad de fluido que pasa por cualquier sección en un cierto tiempo dado es constante, entonces la masa de fluido que pasa por la sección 2 en un tiempo dado será igual a la masa que fluye por la sección 1 en el mismo lapso (pero pasará a velocidad distinta).

Como la masa solo pasa, corre por el tubo, entonces:

La masa inicial (M1) será igual a la masa final (M2)

M1 = M2

Como M = ρ • v • A, donde ρ (densidad) es constante (no cambia) entonces:

ρ1 •  v1 • A1 =  ρ2 •  v2 • A2

Debemos notar que en estas fórmulas usamos la v = vel = velocidad

Si el fluido que circula entre las secciones 1 y 2 es incompresible (ρ1 = ρ2) la ecuación de continuidad se expresa por:

A1 • v1  = A2 • v2

Y como ya vimos que

Q = A • vel,  entonces

Q1 = Q2

Veamos la comprensión de estos conceptos desarrollando un par de ejercicios.

Ejercicio 1:

En la figura se muestra un sistema de tubos (ductos o cañerías)  que lleva agua. La velocidad en la sección 1 (la más ancha = A1) es de 4 m/s y el diámetro de dicha sección es de 25 cm. En la sección 2 (la más angosta = A2) el diámetro es de 10 cm.

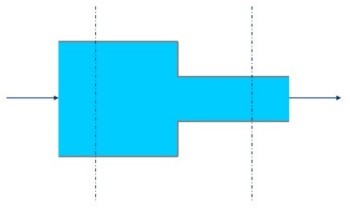
Encuentre o calcule el caudal y la velocidad en la sección 2.

Tenemos las fórmulas

A1 • v1  = A2 • v2 para la velocidad y

Q1 = Q2 para el caudal

Recordemos que si medimos la distancia en metros, el tiempo en segundos y la sección (su área) en metros cuadrados, tendremos el caudal en metros cúbicos por segundo.

Entonces, calculamos el área de la sección 1, de la cual conocemos su diámetro:

25 cm  = 0,25 m (diámetro de la tubería en la sección 1); por lo tanto, su radio es 0,125 m (la mitad del diámetro)

Calculamos su área en m ² .  usando la fórmula de cálculo para el área de un círculo (las cañerías y tubos son siempre circulares):

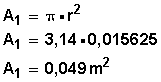
Ahora, calculamos el área de la sección 2 (también conocemos su diámetro):

10 cm = 0,10 m (diámetro de la tubería en la sección 2); por lo tanto, su radio es 0,05 m (la mitad del diámetro)

Calculamos su área en m ² :

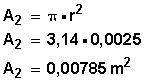
Reemplazamos los valores:

En A1 • v1  = A2 • v2 para la velocidad

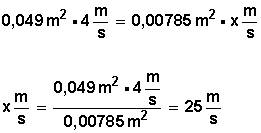
Ahora, reemplazamos en Q1 = Q2 para el caudal:

Recordemos: Si medimos la distancia en metros, el tiempo en segundos y la sección (su área) en metros cuadrados, tendremos el caudal en metros cúbicos por segundo.

Q1 = A1 •  v1

Q2 = A2 • v2

La velocidad del flujo en su paso por la sección 2 es de 25 metros por segundo y el caudal inicial, igual al caudal final, es de 0,196 m ³ por segundo

Ejercicio 2:

Por una tubería de 10 cm de diámetro circula agua a una velocidad de 6 m/s. Si aumentamos al doble el área de la tubería, ¿a qué velocidad circulará el agua por esa sección?

Veamos:

Sabemos que

A1 • v1  = A2 • v2 para la velocidad

Calculamos el área de la sección 1

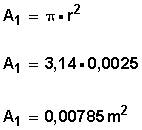
Sabemos que el área de la sección 2 es el doble de la 1; por lo tanto, A2 = 2 • 0,00785 = 0,0157 m ²

Reemplazamos los valores en la fórmula:

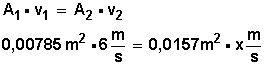
Despejamos x (que nos indicará la velocidad del flujo en la sección 2 de la tubería)

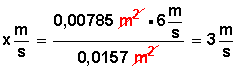
Respuesta: Si aumentamos al doble el área de una tubería, la velocidad del flujo se reduce a la mitad

PSU: Física; Pregunta 37_2010

Ecuación de Bernoulli

Al obstruir parcialmente la salida del agua en una manguera, el agua sale con mayor velocidad.

Pulverizador de insecticida Este pulverizador funciona basado en el comportamiento de los fluidos en movimiento. Se explica su funcionamiento por la Ley de la continuidad y el Principio de Bernoulli.

Ir a: Hidrodinámica - Parte IV

Fuentes Internet:

http://www.sc.ehu.es/sbweb/fisica/fluidos/dinamica/reynolds/reynolds.htm

http://www.lawebdefisica.com/dicc/bernoulli/

http://www.fisicanet.com.ar/fisica/dinamica_fluidos/ap01_hidrodinamica.php

http://webdelprofesor.ula.ve/ciencias/labdemfi/fluidos/html/fluidos.html

http://www.sc.ehu.es/sbweb/fisica/fluidos/dinamica/bernoulli/bernouilli.htm