Descomposición de una fuerza

Para resolver muchos problemas sobre fuerzas, tanto gráfica como analíticamente, hay que saber descomponer una fuerza en otras dos orientadas según los ejes de coordenadas (x e y) , cuyos efectos sumados sean iguales a la fuerza que estamos descomponiendo.

En los sistemas de fuerzas estudiados anteriormente conocíamos las componentes (F1 y F2) y calculábamos la resultante (R).

En la descomposición de fuerzas , conocemos la resultante (R) y nos interesa conocer sus componentes (F1 y F2 sobre las coordenadas x e y) .

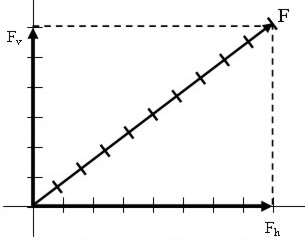
Descomposición gráfica de una fuerza en componentes perpendiculares: Fh, sobre el eje horizontal (la coordenada x) y Fv, sobre el eje vertical (la coordenada y).

La descomposición de una fuerza en sus componentes se puede hacer sobre cualquier dirección. Sin embargo, lo más frecuente es descomponer una fuerza en direcciones perpendiculares (horizontal y vertical, ejes coordenados).

Para ello, la fuerza dada se coloca en el origen de unos ejes coordenados y desde el extremo (flecha) de la fuerza se trazan líneas perpendiculares a los ejes, como se indica en la figura superior.

Las distancias desde el origen hasta esas perpendiculares nos dan la medida de las componentes horizontal y vertical de la fuerza dada.

Entonces: Las proyecciones sobre los ejes son sus componentes.

Hasta aquí tenemos la solución o representación gráfica de fuerzas.

Solución analítica o matemática

En seguida abordaremos la solución o cálculo del valor (módulo) de una fuerza y sus componentes (solución analítica o matemática).

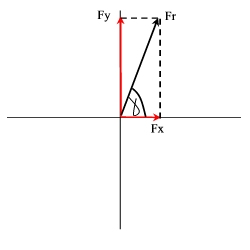
Para resolver este tipo de problemas, lo que hay que hacer es proyectar sobre los ejes la fuerza dada (figura de arriba) y calcular, por medio de relaciones trigonométricas simples, tales como seno, coseno y tangente , el valor de sus componentes y el valor del ángulo de aplicación.

Una vez que tenemos cada componente proyectada y hechos los cálculos, hacemos las sumas y restas sobre cada eje para luego volver a componer todo en una nueva resultante.

Para hallar la resultante total nueva hay que realizar el procedimiento inverso; es decir, componer las dos fuerzas.

El módulo de la nueva resultante se calcula como la raíz cuadrada de la suma de cada componente al cuadrado:

El ángulo se puede calcular con la tangente:

Veamos:

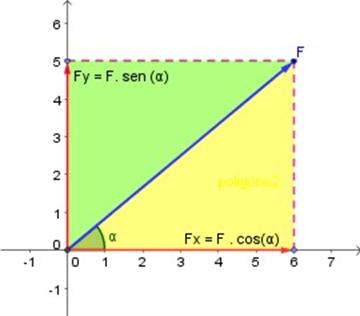
Aplicando la definición de seno al ángulo ( α en nuestro dibujo ilustrativo de arriba) que forman el vector con el eje x (en un triángulo rectángulo el seno es el cateto opuesto al ángulo dividido por la hipotenusa), y de coseno que es el cateto adyacente dividido por la hipotenusa, podemos calcular las componentes (el valor que toma la fuerza en su proyección hacia los ejes x e y ):

Fx = F• cos α

se lee: la componente Fx de la fuerza original (F) es igual al producto entre esta fuerza y el coseno del ángulo (α) que forma con su propia proyección en x.

Fy = F• sen α

se lee: la componente Fy de la fuerza original (F) es igual al producto entre esta fuerza y el seno del ángulo (α) que forma con su propia proyección en y.

Las componentes Fx (proyección color amarillo) y Fy (proyección color verde) son las proyecciones de F sobre los ejes de coordenadas y son también vectores.

Entonces, cuando conocemos las componentes de F sobre los ejes, no sólo conocemos la orientación (el ángulo con el eje x define su dirección), sino que podemos hallar su módulo usando las relaciones trigonométricas descritas.

Veamos un ejemplo:

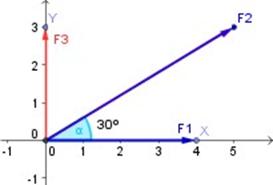
Tenemos tres fuerzas en distintas direcciones, como se indica en el gráfico siguiente:

F1 sobre el eje X,

F2 a 30° del eje X y

F3 sobre el eje Y.

Donde:

F1 = 40 N

F2 = 70 N

F3 = 30 N

α = 30º

Lo que debemos hacer primero es descomponer las fuerzas para luego calcular la sumatoria de las fuerzas en X y luego la sumatoria en Y.

Para las fuerzas en X vemos que F1 ya está sobre el eje X y mira a la derecha es decir, es positiva.

La F2 es más complicada porque no está sobre ningún eje, sin embargo, se la puede descomponer proyectándola en cada uno de los ejes.

Con el coseno se obtiene su componente (su valor) proyectado sobre X

coseno , es la razón (división) entre el cateto adyacente al ángulo y la hipotenusa:

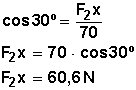
Fuerzas_Descomponer003

Nota: el valor del cos30º lo obtenemos en la calculadora: apretamos la tecla cos , luego anotamos 30 y apretamos el signo igual ; el resultado lo multiplicamos por 70 para obtener los 60,6 N.

Entonces, la suma de fuerzas en x (Fx) será 40 N (F1, que ya está en x) más 60,6 N (valor de la componente de F2 proyectada en la x):

Fx = F1 + F2x

Fx = 40 N + 60,6 N = 100,6 N

Ahora, con el seno se obtiene la componente (el valor de la F2 ) proyectado sobre Y.

Seno , es la razón (división) entre el cateto opuesto al ángulo y la hipotenusa

Fuerzas_Descomponer004

Nota: el valor del sen30º lo obtenemos en la calculadora: apretamos la tecla sin , luego anotamos 30 y apretamos el signo igual ; el resultado lo multiplicamos por 70 para obtener los 35 N.

Fy = F3 + F2y

Fy = 30 N + 35 N = 65 N

Tenemos ahora solo dos fuerzas la Fx (100,6 N) y la Fy (65 N) . Entonces podemos usar la fórmula de Pitágoras para hallar la resultante, que sería la hipotenusa en el teorema de Pitágoras .

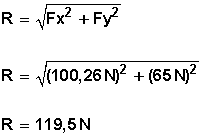
Fuerzas_Descomponer005

Este es el valor de la resultante. Es su módulo, pero no sabemos el valor de su ángulo con respecto al eje x. Lo podemos hallar con la tangente.

Sabemos, sin hacer cálculos, que al ser Fx y Fy positivas la R debe caer en el primer cuadrante de los ejes.

tangente , es la razón entre el cateto opuesto al ángulo y el cateto adyacente al mismo.

Calculadora científica para hacer las operaciones complejas.

Este es el valor de la función tangente (0,646) pero no el valor del ángulo. Para el valor del ángulo hacemos la inversa y arroja el valor de:

α = 32, 86°

Nota: Para obtener la inversa de la función tangente, en la calculadora científica: apretamos Shift , luego apretamos tan , introducimos el valor (0,646 en este caso) y apretamos el signo = (igual) .

Tendremos el resultado en grados (valor del ángulo formado por la fuerza resultante y la ordenada x)

Ejercicios:

Calcular gráficamente y analíticamente las componentes horizontal y vertical de cada una de las siguientes fuerzas conociendo su intensidad y el ángulo que forma la fuerza con el eje horizontal.

1) 25N y 15o.

2) 8N y 20o.

3) 10N y 45o.

4) 6N y 30o.

5) 12N y 60o.

Volver a: Sistemas de fuerzas

Fuentes Internet:

http://recursostic.educacion.es/secundaria/edad/4esofisicaquimica/impresos/quincena3.pdf

http://recursostic.educacion.es/secundaria/edad/4esofisicaquimica/4quincena3/4q3_contenidos_1a.htm

Ver:

http://fisicaparatodo.files.wordpress.com/2011/02/vectores-no-colineales1.pdf

http://recursostic.educacion.es/secundaria/edad/4esofisicaquimica/impresos/quincena3.pdf