Polígonos |
Polígono, definición
Un polígono es una figura geométrica plana cerrada, formada completamente por segmentos de líneas que se intersectan en sus extremos. A estos segmentos se les llama lados . Los polígonos pueden tener cualquier cantidad de lados y ángulos, pero sus lados nunca pueden ser curvos.
La manera más fácil de identificar un polígono es viendo si es una figura cerrada sin lados curvos. Si existe alguna curvatura en la figura, no puede ser un polígono.
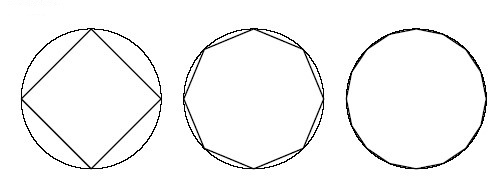
El intento de aproximarse a un círculo usando incluso un polígono con un número astronómico de lados, fallará, pues cada lado minúsculo sigue siendo recto, en tanto que el círculo que puede circunscribirse pasando por cada punto del polígono, sigue siendo curvo en ese intervalo.
|
|
Aunque visualmente parezca un círculo, cada intervalo entre dos puntos será curvo.
|
La palabra polígono está formada por dos voces de origen griego: “polys”: muchos y “gonía” : ángulos; por lo tanto, es una figura con varios ángulos.
También se define como una poligonal cerrada.
El polígono más pequeño es el triángulo, que tiene tres lados y tres ángulos.
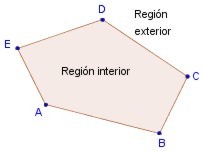
El polígono es la frontera que separa al plano en dos regiones: una que está dentro, llamada región interior del polígono y una exterior, llamada región exterior del polígono. El plano es la unión de estos tres subconjuntos.
|
Un polígono está formado por elementos básicos. Éstos son:
1. vértice
2. lado
3. ángulo interior
4. ángulo exterior
5. diagonal
|
|
1. Vértice : es el punto de intersección de dos segmentos contiguos. Se designan con una letra mayúscula A, B, C, D...
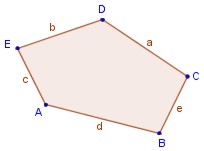
2. Lados: es cada uno de los segmentos de recta que forman el polígono. Se designa con dos letras mayúsculas ubicadas en sus extremos, o con una letra minúscula en correspondencia con el vértice opuesto: AB = d, BC = e , CD = a, DE = b, EA = c
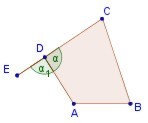
3. Ángulo interior: es el ángulo formado por dos lados del polígono. El ángulo interior se designa con una letra griega o con las tres letras mayúsculas de los vértices que correspondan.
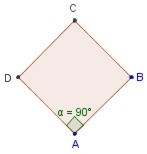
4. Angulo exterior: es el ángulo formado por un lado y la prolongación de otro contiguo hacia la región exterior. Generalmente se designa con la letra griega del ángulo interior adyacente acompañada de un subíndice
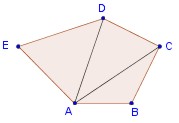
5. Diagonal: es el trazo que une dos vértices no consecutivos del polígono. Se designa con las dos letras mayúsculas correspondientes a los vértices que se unen, o por una letra d con subíndice: AC =d 1, AD = d 2.
Apotema de un polígono regular
La apotema de un polígono regular es el segmento perpendicular a un lado desde el centro del polígono. Es básica para conocer el área del polígono ya que es la altura de cada uno de los triángulos formados por cada dos radios y el lado.
Elementos secundarios de un polígono
En todo polígono (el triángulo es un polígono) podemos obtener elementos secundarios como:
Bisectrices, se denomina bisectriz al rayo que dimidia al ángulo, es decir, lo divide en 2 partes iguales.
Simetrales, la simetral es una recta perpendicular que dimidia a un trazo.
Alturas, una altura, cuyo símbolo es h, es el trazo perpendicular que une un lado del triángulo con el vértice opuesto.
Transversales, la transversal es el segmento que une el punto medio de un lado con el vértice opuesto.
Medianas, son los segmentos que unen los puntos medios del triángulo.
Ver:
Polígono inscrito y circunscrito
Polígonos: nombres de polígonos
Polígonos regulares: perímetro y área
Fuentes Internet:
CK-12 Geometría – Edición española – 2011, editado por CK-12 Foundation.

