PSU: Geometría |
|
Pregunta 09_2005
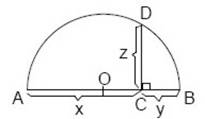
En la figura, el trazo AB (
![]() ) es el diámetro de la semicircunferencia de centro O,
) es el diámetro de la semicircunferencia de centro O,
![]() , entonces ¿cuál(es) de las afirmaciones siguientes es(son)
siempre
correcta(s)?
, entonces ¿cuál(es) de las afirmaciones siguientes es(son)
siempre
correcta(s)?
I) x : z = z : y
II) x : z = z : (x + y)
III) x : y = y : z
Alternativas
A) solo I
B) solo II
C) solo III
D) solo I y III
E) ninguna de ellas
Curso: Tercero medio
Tema: Proporcionalidad en el triángulo rectángulo
Comentario:
Lo primero que el alumno debe ser capaz de deducir es que al unir los puntos A, D y B se forma el Δ ABD rectángulo en D, pues está inscrito en una semicircunferencia.
Para analizar las tres proporciones que se presentan (I, II y III) debe recordar materia de Tercero medio sobre proporcionalidad en el triángulo rectágulo relativa a la altura, enunciado en el Teorema de Euclides , cuyo enunciado dice:
“La altura correspondiente a la hipotenusa de un triángulo rectángulo es media proporcional geométrica entre las proyecciones de los catetos sobre la hipotenusa.”
|
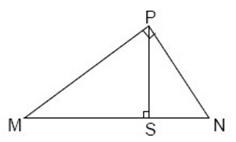
Lo anterior se explica de la siguiente manera:
en el
Δ MNP
(figura a la derecha), la altura correspondiente a la hipotenusa
(MN)
es
PS
, la proyección del cateto
MP
sobre la hipotenusa
MN
es
MS
y la proyección del cateto
PN
sobre la misma hipotenusa es
SN
, luego, el teorema queda expresado así:
![]()
Aplicando esta sencilla relación se comprueba que la afirmación I) es verdadera.
Si la aplicamos a los datos de la figura tenemos:
![]()
que corresponde a x : z = z : y , luego la respuesta correcta está en A. Analizando los otras dos proporciones se comprueba que no se cumplen.
En general, los problemas de geometría resultan difíciles para los estudiantes. En este ítem hubo una omisión del 56,4 por ciento, y casi el 20 por ciento de quienes la respondienron marcó la opción E.
Fuente Internet:
Publicación oficial del Demre en www.demre.cl

