PSU: Estadística y Probabilidades |
Pregunta 03_2006
La tabla adjunta
|
Edad (en años) |
15 |
16 |
17 |
18 |
19 |
|
Alumnos |
50 |
40 |
60 |
50 |
20 |
muestra las edades de 220 alumnos de un colegio. ¿Cuál(es) de las siguientes afirmaciones es(son) verdadera(s)?
I) La moda es 17 años.
II) La mediana es mayor que la media (promedio).
III) La mitad de los alumnos del colegio tiene 17 ó 18 años.
Alternativas
A) Sólo I
B) Sólo II
C) Sólo I y III
D) Sólo II y III
E) I, II y III
Contenido: Medidas de tendencia central , como son la media aritmética (promedio), la mediana y la moda.
Comentario
Debe recordar que la moda es la medida de mayor frecuencia (el valor que más se repite), en este caso, según la tabla, la mayor frecuencia de alumnos es 60 y corresponde a los de 17 años, por lo tanto I) es verdadera .
Para analizar II), debe determinar el promedio y compararlo con la mediana .
En este caso, es el promedio para datos agrupados y se resuelve de la siguiente forma:
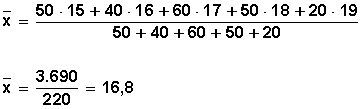
La mediana es el valor de la variable que queda en el punto medio de una serie, después de que las medidas o puntajes que la integran han sido colocados en orden según su magnitud. En otros términos, la mediana es el valor por encima y por debajo del cual queda el 50 por ciento de los casos.
Al calcular la frecuencia acumulada de la tabla se tiene:
|
Edad |
Alumnos |
Frecuencia
|
|
15 |
50 |
50 |
|
16 |
40 |
90 |
|
17 |
60 |
150 |
|
18 |
50 |
200 |
|
19 |
20 |
220 |
Buscamos la mitad del número total de casos, que corresponde a
![]() .
.
Así la mediana es 17 , pues es el primer valor de la variable cuya frecuencia acumulada es mayor que la mitad del número de datos (150 es mayor que 110).
Luego, la mediana es mayor que el promedio (17 es mayor que 16,8), por lo que II) es verdadera .
Los alumnos son 220 y los que tienen 17 ó 18 años corresponden a la suma de los alumnos de estas edades; es decir, 110, que corresponde a la mitad del total, por lo que la III) es verdadera.
Luego la opción correcta es E) .
El 46 por ciento de las personas abordaron la pregunta en forma correcta y la omitió casi la cuarta parte (24 por ciento).
Fuente Internet:
Publicación oficial del Demre en www.demre.cl

