Logaritmo |
El logaritmo de un número, en una base dada, es el exponente al cual se debe elevar la base para obtener el número.
Se lee “logaritmo de x en base a es igual a y ”, pero debe cumplir con la condición general de que a (la base) sea mayor que cero y a la vez distinta de uno :
Para aclarar el concepto, podríamos decir que logaritmo es solo otra forma de expresar la potenciación, como en este ejemplo:
Que leeremos: logaritmo de 9 en base 3 es igual a 2
Esto significa que una potencia se puede expresar como logaritmo y un logaritmo se puede expresar como potencia.
El gráfico siguiente nos muestra el nombre que recibe cada uno de los elementos de una potencia al expresarla como logaritmo:
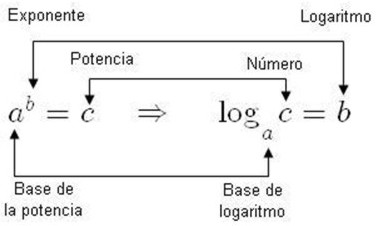
Ver: PSU: Matemática; Pregunta 19_2006
Entonces, podemos preguntar: ¿Que es el logaritmo?
El logaritmo es " el exponente " por el cual se ha elevado una base para obtener la potencia .
Ejemplos:
1)
El resultado (2) es el exponente por el cual debemos elevar la base (2) para obtener la potencia (4): 2
2
= 4
2)
El resultado (0) es el exponente por el cual debemos elevar la base (2) para obtener la potencia (1): 2
0
= 1
3)
El resultado (y) es el exponente por el cual debemos elevar la base (1/2) para obtener la potencia (0,25):
, pero en este caso debemos despejar el exponente
y:
4)
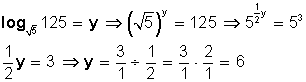
5)
Cuidado con esto, hay que recordarlo: Cuando la base no aparece expresada se supone que ésta es 10:
, el
10
que indica la base, no se coloca, se supone, así:
6)
Aquí, otra nota importante, para no olvidar: Los logaritmos que tienen base e se llaman logaritmos neperianos o naturales. Para representarlos se escribe ln o bien L . La base e está implícita, no se escribe:
7)
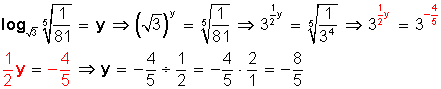
Con lo ya expuesto, podemos empezar a establecer las:
Propiedades de los logaritmos
No existe el logaritmo de un número con base negativa.
No existe el logaritmo de un número negativo.
No existe el logaritmo de cero.
El logaritmo de 1 es cero.
El logaritmo de a en base a es uno.
El logaritmo en base a de una potencia en base a es igual al exponente.
Ver: PSU: Matemática;
Pregunta 31_2010
El logaritmo de un producto es igual a la suma de los logaritmos de los factores:
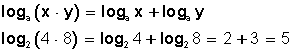
El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor:
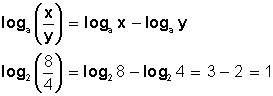
El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base:
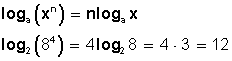
Ver: PSU: Matemática; Pregunta 17_2005
El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz:
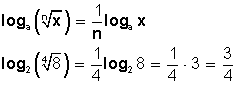
Cambio de base:
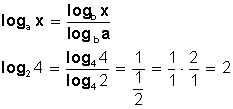
Logaritmos decimales:
Son los que tienen base 10 . Se representan por log (x) (ya vimos que la base 10 no se escribe, queda implícita).
Logaritmos neperianos o naturales:
Son los que tienen base e . Se representan por ln (x) o L(x) (ya vimos que la base e tampoco se escribe, s e subentiende cuando aparece ln ) .
Algunos ejemplos de logaritmos neperianos son:
ln 1 = 0 ; puesto que e 0 = 1
ln e 2 = 2 ; puesto que e 2 = e 2
ln e −1 = −1 ; puesto que e −1 = e −1
El número e tiene gran importancia en las Matemáticas. No es racional (no es cociente de dos números enteros) y su valor, con seis cifras decimales, es
e = 2,718281...
Ver: Historia de los logaritmos
Fuentes Internet:
http://www.vitutor.com/al/log/log.html
Ver en Youtube:
http://www.youtube.com/watch?v=G4cNYRaYw3A&feature=related