El Teorema del Factor es una aplicación que se utiliza para resolver el Teorema del Resto (o del residuo); por lo tanto, funcionan juntos.

El Teorema del Factor establece que un polinomio, que llamaremos P(x), tiene un factor (x – a) sí, y solo sí, f(a) = 0.

O, dicho de otro modo, un polinomio (x – a) será factor de otro polinomio sí, y solo sí, f(a) = 0.

Comprobado como factor, el o los valores de “a” son raíces o soluciones de la ecuación dada.

Entonces, podemos decir que con el Teorema del Factor podemos analizar las ecuaciones polinómicas, probando con diferentes valores para “a”.

También se puede emplear el Teorema del Factor para factorizar completamente un polinomio en el producto de n factores.

A la par, tenemos al Teorema del Resto o del residuo, que es bastante útil para evaluar polinomios a un valor dado de x.

Ver: Teorema del resto

El Teorema del Resto establece que cuando un polinomio, P(x), se divide por un polinomio lineal, x – a, el resto de dicha división tiene que ser equivalente a f(a).

Vale la pena acotar que el teorema del resto solo opera cuando una función se divide por un polinomio lineal, el cual tiene la forma x + n, o x – n.

El teorema del factor se presenta como el reverso del teorema del resto, ya que para que un factor x – a divida sintéticamente un polinomio P(x), debe arrojar un resto igual a cero; o  sea, x  -  a  = 0.

Veamos un ejemplo:

Dada la función

f(x) = x² – 5x + 6, comprobar si x – 1 es factor de la ecuación x² – 5 x + 6 = 0

¿Cómo operamos?, simplemente reemplazamos cada x  de la ecuación por el valor –1 del polinomio x –  1, con signo cambiado (como es – 1, colocamos +1).

1² – 5(+1) + 6 = 0

1 – 5  +   6  =  2  (distinto de cero; por tanto, no es factor)

Ahora, comprobar si x –  2 es factor de la misma ecuación:

Reemplazamos cada x  de la ecuación por el valor –2 del polinomio x –  2, con signo cambiado (como es – 2, colocamos +2).

x²  – 5 x + 6 = 0

2²  – 5(+2) + 6 = 0

4  – 10  + 6  = 0 (resto cero; por tanto, sí es factor, y a su vez el 2 es una raíz o solución de la ecuación analizada)

Ahora, comprobar si  x –  3 es factor de la misma ecuación:

Reemplazamos cada x  de la ecuación por el valor –3 del polinomio x –  3, con signo cambiado (como es – 3, colocamos +3).

x² – 5 x + 6 = 0

3² – 5(+3) + 6 = 0

9 – 15  +  6  = 0  (resto cero; por tanto, sí es factor, y a su vez el 3 también es una raíz o solución de la ecuación analizada).

Como un ejercicio probatorio, resolvamos por la fórmula general la ecuación de segundo grado x² – 5 x + 6 = 0:

Recordemos que la fórmula general para una ecuación de la forma ax²  + bx  +  c es

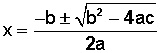
En nuestro ejemplo
a  =  1

b  = –5

c  =  6

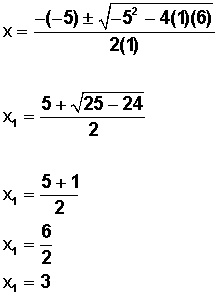
Y para x₂:

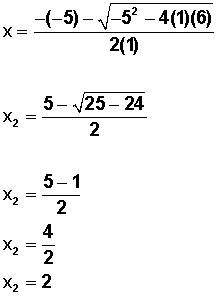
Las soluciones para esa ecuación de segundo grado son:

x   =  3

x  = 2

Lo que ya habíamos comprobado usando el Teorema del Factor; el cual, como vemos, también puede usarse como una manera más sencilla de resolver una ecuación cuadrática.