Para resolver problemas de conversión de medidas en el Sistema Métrico Decimal

Si no tenemos a la vista el cuadro con las equivalencias debemos aplicar la siguiente metodología para hacer conversiones de magnitudes en el Sistema Métrico Decimal :

Primero

Si vamos de una magnitud grande a una más pequeña, el valor conocido lo multiplicamos por un múltiplo de diez (10, 100, 1.000 o 10.000)

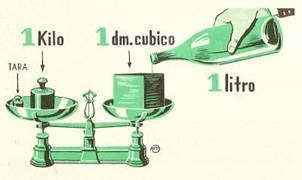
Segundo

Para decidir qué múltiplo de diez usaremos, debemos saber el orden de las magnitudes de mayor a menor, como se indica en el siguiente cuadro:

1	2	3	4	5	6	7
Km Kl Kg	Hm Hl Hg	Dm Dl Dg	m l g	dm dl dg	cm cl cg	mm ml mg

¿Por qué es importante saber este orden?

¿Mide 70 cm o 7 dm?

Si vamos a convertir Km a cm , por ejemplo, contamos los lugares que separan a ambas magnitudes (en el conteo se excluye el lugar que ocupe una de elllas, pero se incluye el lugar de la otra):

Un ejemplo:

Entre Km y cm hay 5 lugares (Hm, Dm, m, dm y cm) , entonces debemos multiplicar por 100.000 ( el 1 seguido de cinco ceros, uno por cada lugar que las separa ).

Tercero

Si vamos de una magnitud pequeña a otra más grande, el valor conocido lo dividimos por un múltiplo de diez (10, 100 , 1.000 o 10.000)

Un ejemplo:

Entre dm y Km hay 4 lugares (m, Dm, Hm y Km) , entonces debemos dividir por 10.000 ( el 1 seguido de cuatro ceros, uno por cada lugar que las separa )

Importante

En el caso de las medidas de longitud, de capacidad y de masa (peso) usaremos múltiplos de diez con un cero por cada lugar que las separa .

En el caso de las medidas de superficie (Km ² , Hm ² , Dm ² , m ² , dm ² , cm ² y mm ² ) usaremos múltiplos de diez agregando dos ceros por cada lugar que las separa.

1	2	3	4	5	6	7
Km 2	Hm 2	Dm 2	m 2	dm 2	cm 2	mm 2

Ejemplo:

Convertir 4 Km ² a m ² .

Entre Km ² y m ² hay tres lugares, entonces  hacemos 4 • 1.000.000 = 4.000.000 m ² (las separan tres lugares, ponemos dos ceros por cada lugar, son seis ceros ).

En el caso de las medidas de volumen (Km ³ , Hm ³ , Dm ³ , m ³ , dm ³ , cm ³ y mm ³ ) usaremos múltiplos de diez agregando tres ceros por cada lugar que las separa.

1	2	3	4	5	6	7
Km 3	Hm 3	Dm 3	m 3	dm 3	cm 3	mm 3

Ejemplo:

Convertir 6.000.000 m ³ a Hm ³ (recordar además que un Hm ³ es igual a una hectárea).

Entre m ³ y Hm ³ hay dos lugares, entonces hacemos 6.000.000 : 1.000.000 = 6 Hm ³ (las separan dos lugares, ponemos tres ceros por cada lugar, son seis ceros )

Fuente Internet:

http://rafamartinaguilera.blogspot.com/2009_02_01_archive.html

Ir a:

Sistema Métrico Decimal